1) cylindrial polar coordinate system
柱面极坐标系
2) cylindrical polar coordinates
柱面极坐标
3) bipolar cylindrical coordinates
双极柱面坐标
4) cylindrical polar coordinates
柱极坐标
5) elliptic cylinder coordinate system
椭圆柱面坐标系
6) Parabolic Cylindrical Coordinate System
抛物柱面坐标系
补充资料：极坐标系
| 极坐标系 polar coordinates 在平面内由极点、极轴和极径组成的坐标系。在平面上取定一点O，称为极点。从O出发引一条射线Ox，称为极轴。再取定一个长度单位，通常规定角度取逆时针方向为正。这样，平面上任一点P的位置就可以用线段OP的长度ρ以及从Ox到OP的角度θ来确定，有序数对（ρ，θ）就称为P点的极坐标，记为P（ρ，θ）；ρ称为P点的极径，θ称为P点的极角。当限制ρ≥0，0≤θ＜2π时，平面上除极点Ο以外，其他每一点都有唯一的一个极坐标。极点的极径为零 ，极角任意。若除去上述限制，平面上每一点都有无数多组极坐标，一般地 ，如果（ρ，θ）是一个点的极坐标 ，那么（ρ，θ＋2nπ），（－ρ，θ＋（2n＋1）π），都可作为它的极坐标，这里n 是任意整数。平面上有些曲线，采用极坐标时，方程比较简单。例如以原点为中心，r为半径的圆的极坐标方程为ρ＝r 等速螺线的方程为 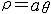 。此外，椭圆 、双曲线和抛物线这3种不同的圆锥截线，可以用一个统一的极坐标方程表示。
|
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条