1) Lorentz bilinear covariant
洛伦兹双线协变量
2) Lorentz-invariant
洛伦兹不变量
3) Lorentz transformation covariance
洛伦兹变换协变性
1.
It is able to teach relativity dynamics by Lorentz transformation covariance in engineering physics, since the college students have learned Galilean transformation covariance and linear algebra already, when they studied relativity theory.
讲相对论时学生已具有伽里略变换协变性和线性代数的知识 ,因此在工科物理中由洛伦兹变换协变性出发讲相对论动力学是可行的 。
4) Lorentz transformation
洛伦兹变换
1.
According to Lorentz transformation,the relativistic covariant of electromagnetic field tensor and 4-dimension forces,and the relativistic invariance of electric charge,it can be directly proved that a moving magnetic monopole will be acted- by a magnetic Lorentz force,and that the magnetic Lorentz force has the same accuracy as the Coulomb low.
概述了磁单极概念的历史发展,从洛伦兹变换出发,利用电磁场张量和四维力的协变性以及电荷相对论不变,直接证明了运动磁单极受磁洛伦兹力,建议了一个磁洛伦兹力的验证方案,并用磁洛伦兹力公式导出狄拉克电荷量子化条件。
2.
Does the theory of special relativity have its experimental foundation? Can it be proved by experiments? Does the relativity about the expansion of time and space contraction exist? Is the Lorentz transformation relative or absolute? These questions are discussed and analysed in this article.
就狭义相对论有无实验基础,能否用实验来证实狭义相对论,时间膨胀、空间收缩的相对性是否存在,洛伦兹变换是相对的还是绝对的等一系列问题进行了分析和讨论,并得出了这样的结论:目前在文献中所能查到的实验没有一个符合爱因斯坦所提出的要求,这些实验只能证实时间膨胀是存在的并且具有绝对性,但不能证实相对论的正确性。
5) Lorentz transform
洛伦兹变换
1.
The Assumption of Using Lorentz Transform to Establish the Two Signs Space and Time Coordinate;
利用洛伦兹变换创建双标度时空坐标的设想
2.
The Lorentz transformation equations directly form the postulates of special relativity.
基于传统文献利用线性变换和间隔不变性导出相对论时空坐标变换关系 ,但对变换式y′ =y ,z′ =z均未加证明 ,提出了另一种洛伦兹变换式的推导方法 ,从两个不同惯性系Σ和Σ′同时观测同一事件P ,利用光速不变原理 ,导出了在不同惯性系中的特殊洛伦兹变换式和一般情况下的洛伦兹变换式 ,并说明了一般情况下的洛伦兹变换式转换为特殊洛伦兹变换式的条
6) Lorenz transformation
洛伦兹变换
1.
According to Lorenz transformation on four-dimension wave vector,the action of light reflection on the movement mirror is analyzed in details.
利用四维波矢量的洛伦兹变换,对光在运动镜面上的反射行为作了详细的分析,推导出此情形下入射角与反射角、入射光频率与反射光频率之间的关系。
补充资料：洛伦兹
| 洛伦兹(1853～1928) Lorentz，Hendrik Antoon 荷兰物理学家。1853年7月18日生于阿纳姆，1928年2月4日卒于哈勒姆。少年时就对物理学感兴趣，还广泛地阅读历史和小说，并熟练地掌握多门外语。1870年他考入莱顿大学，学习数学、物理和天文。1875年获博士学位。1877年莱顿大学聘请他为理论物理学教授（这个职位最早是为J.D.范德瓦尔斯设的），在该校任教35年，他对物理学的贡献都是在这期间作出的。1912年他辞教职到哈勒姆担任博物馆顾问，并兼任莱顿大学名誉教授。 1919～1926年他还在荷兰政府的教育部门工作。1921年起任高等教育部部长。1911～1927年担任索尔维物理学会议的固定主席。洛伦兹除了获得诺贝尔物理学奖以外，还被英国皇家学会授予朗福德奖章和科普利奖章。法国巴黎大学和英国剑桥大学都曾授予他名誉教授称号，他还被选为德国物理学会会员和英国皇家学会会员。爱因斯坦曾称他为“我们时代最伟大和最崇高的人”。 洛伦兹在物理学上最重要的贡献是他的电子论。他的博士论文是用J.C.麦克斯韦的电磁理论来处理光在介质界面上的反射和折射问题。文末，他提到把光的电磁理论与物质的分子理论结合起来的前景，这就是他后来创立电子论的根源。1878年他发表了光与物质相互作用的论文，认为以太是静止的，无所不在的，而普通物质的分子则都含有带电的谐振子，导出了分子折射率的公式（洛伦兹-洛伦茨公式）。1892年他开始发表电子论的文章，认为一切物质的分子都含有电子，电子对于以太是完全透明的，以太与物质的相互作用归结为以太与物质中电子的相互作用。1895年他提出了著名的洛伦兹力公式。1892年他研究过地球穿过静止以太所产生的效应，为了说明迈克耳孙-莫雷实验的结果，他独立地提出了长度收缩的假说。1895年他发表了长度收缩的准确公式，即在运动方向上，长度收缩因子为 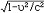 。1896年P.塞曼发现放在磁场中的光源其光谱线发生分裂（塞曼效应）。洛伦兹立即用他的电子论对此现象作了定量解释。为此，他和塞曼共获1902年的诺贝尔物理学奖。1899年他论述了惯性系之间坐标和时间的变换问题，并得出电子质量与速度有关的结论。1904年他发表了著名的变换公式（J.-H.庞加莱首先称之为洛伦兹变换）和质量与速度的关系式，并指出光速是物体相对于以太运动速度的极限。在1911年他指出，用经典物理学所涉及的最普遍方式无法导出符合实际的黑体辐射公式，这无疑是对普朗克量子论的一种变相承认和有力促进。他在热力学、物质分子动理论和引力理论等方面都有过贡献。1878年他曾指出物理学研究的目的是找出一些基本的原理，使得所有的现象都能用这些原理来解释。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条