1) radiantly unbounded function


放射无界函数
3) approximation of unbounded functions


无界函数逼近
1.
On Grwald interpolation polynomial operators and approximation of unbounded functions;


Grwald插值多项式算子与无界函数逼近
4) unbounded initial value


初值函数无界
5) unbounded continuous functions


无界连续函数
1.
By applying the classical appropriate functions 1, x x2 to the method of multiplier- enlargement, this paper established a certain theorem to approximate any unbounded continuous functions by modified positive linear operators.
将经典“试探函数组”1,x,x2应用于扩展乘数法;建立了一个判别线性正算子能否改造为逼近任意无界连续函数的充要条件。
6) function of unbounded variation


无界变差函数
补充资料:有界变差函数
| 有界变差函数 bounded variation,function of 定义在区间[a,b]上,并能表为两个单调增函数之差的实值函数。属常用的函数类,它有许多好的性质,例如:有界变差函数必为有界函数;两个有界变差函数的和、差、积仍为有界变差函数;有界变差函数在[a,b]上黎曼可积;有界变差函数在[a,b]上几乎处处可导,导函数在[a,b]上勒贝格可积。此外还有,平面上由y=f(x)表示的曲线C可求长的充分必要条件是f为有界变差函数。应注意的是,连续函数不一定为有界变差函数。例如: 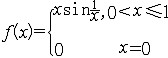 。 。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条