1) mathematical bases of the visualization


可视化数学基础
2) basic stereology


基础体视学
3) Mathematical basis


数学基础
1.
This paper not only discusses the mathematical basis of the superpose principle but also summarizes its usage in physics.
讨论了叠加原理的数学基础,概述了叠加原理在物理中的应用,并指出叠加原理不是一条普遍的原理。
2.
For the need of mapmaking,the passage discusses some of the mathematical basis of oblique coordinate system,including the concept of constitution,calculating formular and the transformation with coordinate system in right angle etc.
从制图需要出发,论述了斜角坐标系的构成原理、计算公式以及与直角坐标系之间的换算关系等数学基础。
4) foundation of mathematics


数学基础
1.
View from the foundation of mathematics, this article analyzed the process of mathematics epistemology: the context of Justification in foundationalism of mathematics; Poincaréand etc Discovery view; sociological view of mathematics that drawing together the contexts of Justification and of Discovery.
从数学基础研究的角度看,数学认识论的发展经历了从数学基础主义的“确证”观到庞加莱、皮亚杰等人的数学的“发现”的认识观,直至数学社会学理论中所强调的“确证”与“发现”相结合的数学认识观。
2.
In the dispute about the foundation of mathematics in the 20th century, philosophers approving Intuitionalism usually take Kant for the originator of their theory.
在20世纪关于数学基础的争论当中,直觉主义流派往往将康德认作是其理论的鼻祖。
5) mathematical foundation


数学基础
1.
The appearance of Russell s paradox causes the crisis of mathematical foundation.


这是因为罗素悖论的出现造成数学基础的危机,在循着如何排除悖论的思路进行数学基础研究所取得成果的基础上,数理逻辑中相继出现了三个划时代的成就,从而推动了数理逻辑的主要分支“四论”的产生和发展。
6) mathematic basis


数学基础
1.
Combining with correlative mathematical methods,mathematic basis of some typical ancient maps in China was investigated,and the course of recognizing the geographical space-dimension in ancient China was analyzed.
从几个典型的中国古地图的数学基础出发,结合相关的数学方法,探讨了中国古人在地理空间维度认知方面走过的历程。
2.
Lunar map projection is the main part of lunar map mathematic basis.


月球地图投影是月球地图数学基础的主要内容,月球地图投影选择与设计是月球测绘的基础性和前瞻性工作。
补充资料:数学基础
| 数学基础 mathematics,foundation of 研究数学的基础,回答“数学是什么?”,“数学的基础是什么?”,“数学是否和谐?”等等一些数学上的根本问题的学科。 发展概况 在数学的发展过程中曾遇到过3次危机。第一次是公元前5世纪毕达哥拉斯学派的希帕索斯发现不可共度线段:正方形的一边与其对角线不可公度,即发现 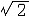 不是有理数。这次危机导致无理数及几何公理系统的建立——欧几里得几何原本诞生。尽管原本还不是严格的公理系统,但它充分表明直观、经验不可全信,几千年来对几何学的研究,特别是后来对非欧几何的研究促使几何学走向严格的公理化。严格公理化的几何就是几何基础也是数学基础的一部分。 不是有理数。这次危机导致无理数及几何公理系统的建立——欧几里得几何原本诞生。尽管原本还不是严格的公理系统,但它充分表明直观、经验不可全信,几千年来对几何学的研究,特别是后来对非欧几何的研究促使几何学走向严格的公理化。严格公理化的几何就是几何基础也是数学基础的一部分。17世纪后半期I.牛顿,G.W.莱布尼兹创立了微积分学,但他们对无穷小的解释很难令人满意,英国主教G.贝克莱抨击当时的微积分,指出它在逻辑上有明显的问题,这便是第二次数学危机。这次危机的出现使数学家们意识到不为微积分建立牢固的基础,只进行运算是不行的。19世纪A.L柯西、K.魏尔斯特拉斯等创立了极限论,以极限为基础建立微积分学。A.鲁宾孙于1960年创立了非标准分析,把实数域扩充到包含无穷小和无穷大的超实数域,圆满解决了“无穷小的矛盾”问题。与此同时,传统逻辑发展为数理逻辑。数理逻辑是数学基础的重要内容。 数学上的第三次危机一般认为始于1902年B.A.W.罗素发现的悖论,后人称这个悖论为罗素悖论:以S表示所有不以自身为元素的集合的全体。按照集合论的概括原则(构成集合的原则),S应该是一个集合。现在问S是否是S的一个元素?如果S∈S,则按照S的定义应有S 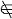 S;如果S S;如果S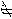 S,则按S的定义又应有S∈S。无论哪种情况都导致矛盾。罗素悖论动摇了集合论,也动摇了当时的数学基础。因为罗素悖论只涉及最基本的集合论概念:集合,元素,属于和概括原则,它的构成十分清楚明白。这个悖论的出现说明以往的朴素集合论中包含矛盾,因而以集合论为基础的整个数学就不能没有矛盾。这个悖论也同时说明数学中采用的逻辑也不是没有问题的。数学上的第三次危机使数学界和逻辑学界都感到问题的严重性。罗素悖论表明不能无条件承认概括原则,然而概括原则的改变将使集合论大为改观,因此对整个数学的影响是巨大的。 S,则按S的定义又应有S∈S。无论哪种情况都导致矛盾。罗素悖论动摇了集合论,也动摇了当时的数学基础。因为罗素悖论只涉及最基本的集合论概念:集合,元素,属于和概括原则,它的构成十分清楚明白。这个悖论的出现说明以往的朴素集合论中包含矛盾,因而以集合论为基础的整个数学就不能没有矛盾。这个悖论也同时说明数学中采用的逻辑也不是没有问题的。数学上的第三次危机使数学界和逻辑学界都感到问题的严重性。罗素悖论表明不能无条件承认概括原则,然而概括原则的改变将使集合论大为改观,因此对整个数学的影响是巨大的。集合论中包含矛盾这个事实,实际上稍早以前就已发现。朴素集合论的创始人G.康托尔,1895年就发现了“最大序数悖论”(所有序数的集合有更大序数);1899年他又发现“最大基数悖论”(所有集合的集合有最大基数,但由这个集合的一切子集构成的集合有更大的基数)。对于这两个悖论当时人们也感到吃惊,但认为这是集合论中的一些技术性问题,只要作一些技术改进就可消除,因此没有引起人们的极大关注。 三次数学危机的发生是数学深入发展的结果,许多数学家为消除危机作了不懈的努力。这些努力促进了数学的发展,特别是促进了数学基础的研究。其中第三次危机对数学的影响更大。人们公认集合论是数学的基础,在数学中有着广泛的应用,任何一门数学都离不开它。非欧几何学的和谐性归结为欧几里得几何学的和谐性;欧几里得几何学的和谐性又归结为实数系统的和谐性;而实数系统的和谐最终归结为集合论的和谐性。但集合论是有矛盾的。第三次数学危机开始时,很多数学家对集合论的改造持旁观态度,认为可由逻辑学家去讨论。后来发现这样行不通,因为在数学论证中每人必须采用某一派的观点,无法回避。 研究学派 自罗素悖论发现以来,对数学基础的研究有三个主要派别:逻辑主义、形式主义和直觉主义。 ①逻辑主义。以罗素和A.N怀特海为代表。他们认为所有数学概念都归结为自然数算术的概念,而算术概念可借助逻辑由定义给出。他们试图建立一个包括所有数学的逻辑公理系统,并由此推出全部数学。逻辑主义认为数学是逻辑的延伸,在罗素的公理系统中不得不引用了非逻辑的选择公理和无穷公理。如果没有这两条公理就无法推导出全部算术,更不用说全部数学。当然,罗素的公理系统充分发展了数理逻辑的公理体系,并且在此基础上展示了丰富的数学内容,对数理逻辑和数学基础的研究起了极大的推动作用,贡献是很大的。②直觉主义。又称构造主义。它的代表人物是L.E.J.布劳威尔。直觉主义者认为数学产生于直觉,论证只能用构造方法,他们认为自然数是数学的基础。当证明一个数学命题正确时,必须给出它的构造方法,否则就是毫无意义的,直觉主义认为古典逻辑是从有穷集合及其子集抽象出来的,把它应用于无穷数学就必然引起矛盾。他们反对在无穷集合中使用排中律。他们不承认实无穷体,认为无穷是潜在的,只不过是无限增长的可能性。可构造性对数理逻辑及计算技术的发展有重要作用。但直觉主义使数学变得非常繁琐复杂。失去了数学的美,因而不被大多数数学家接受。③形式主义。以D.希尔伯特为代表,可以说是希尔伯特的数学观点和数学基础观点。希尔伯特主张捍卫排中律,他认为要避免数学中的悖论,只要使数学形式化和证明标准化。为了使形式化后的数学系统不包含矛盾,他创立了证明论(元数学)。他试图用有穷方法证明各个数学分支的和谐性。1931年K.哥德尔证明了不完全性定理,表明希尔伯特方案不能成功。后来许多人对希尔伯特方案加以改进。W.K.J.基灵利用超限归纳法证明了算术的无矛盾性。在数学基础的研究中,鲁宾孙,P.J.科恩自称为形式主义者(希尔伯特本人不认为自己是形式主义者),他们认为数学所研究的不过是一些毫无内容的符号系统,“无穷集”,“无穷整体”等在客观上是不存在的。希尔伯特的设想虽然没有实现,但却创立了证明论,又促进了递归论的发展,因此对数学基础的研究有很大的贡献。 古代由于科学技术发展水平的限制,无需专门研究数学基础,这种情况一直持续到牛顿、莱布尼兹创立微积分的时代。非欧几何的出现使人们意识到必须为数学建立不依赖于直观的基础,必须研究数学的可靠性,特别是无矛盾性,无公度线段的存在及集合论的悖论说明人们不能只依靠直观,而必须为数学建立严格的逻辑基础,解决数学的哲学基础问题。因此数学基础是包括哲学方法论和逻辑等诸方面问题的学科,数学基础现已形成数学的重要分支之一。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条