1) multi-scale fractal dimensional number
多尺度分维数
2) multi-scale fractal demension
多尺度分维
3) multidimensional scaling
多维尺度分析
1.
Finally,using multidimensional scaling,dimensionality of influencing factors of the soundscape is obtained.
通过现场调查研究了影响声景观评价的各种因素;选取及模拟典型声景观片段,在实验室内采用成对比较法进行主观评价实验,得到关于各声景观素材的不相似度矩阵;再应用多维尺度分析,获得声景观评价影响因素的维度数。
2.
According to the survey data of organisms attached on concrete and iron reefs in September,2008 in Yangmeikeng,Shenzhen,the compositions of common species and the characteristics of the community structure were studied based on principal components analysis,the hierarchical cluster analysis and multidimensional scaling.
根据2008年9月对深圳杨梅坑人工鱼礁区混凝土礁体和铁制礁体上附着生物的调查资料,采用主成分分析、聚类分析和多维尺度分析方法研究了人工鱼礁附着生物组成及群落结构的基本特征。
4) MDS
多维尺度分析
1.
Statistical Shape Classification Based on MDS;
针对物体轮廓曲线,采用新的模与相位保持的傅里叶描述方法,将连续的轮廓曲线降维归一化为RM空间中的点,引入DTW(Dynamic Time Warping)相似度,使用多维尺度分析(MDS),对多类物体基于形状进行聚类。
2.
AN ANALYSIS ON ORGANIZATIONAL MANAGEMENT STRUCTURE OF THE JIN-MERCHANT IN THE MING AND QING DYNASTY WITH MDS;
本研究运用文献资料整理法和多维尺度分析法,对明清晋商组织管理的结构进行了研究。
5) multi-dimension analysis
多维尺度分析
1.
Using the factor analysis,clustering analysis and multi-dimension analysis of the SPSS11.
0的因子分析、聚类分析以及多维尺度分析,对CSSCI中收录的2000-2005年网络信息计量学的109篇被引文献进行了作者共被引分析,归纳了国内网络信息计量学领域的作者群体,指出当前国内主要集中于对网络信息计量学理论、方法和应用的研究。
6) multi-scale fractal parameter
多尺度分形参数
1.
First, a fractal pattern of Mandelbrot set is produced using computer and the pattern is detected by multi-scale fractal parameters with a ideal result.
根据地震波的动力学参数对裂缝敏感性和裂缝的分形特征,以地震层位振幅数据为基础,应用分形理论的裂缝检测方法(多尺度分形参数的地毯覆盖方法)对裂缝进行检测。
2.
According to the sensitivity of dynamical parameters to fracture,the fractal characteristics of fracture,and based on fractal edge detection in image processing, this paper presents two fracture detection methods: multi-scale fractal parameter carpet coverage method and fractal compression method.
依据地震波的动力学参数对裂缝的敏感性和裂缝的分形特征 ,以地震层位振幅数据为检测对象 ,基于图像处理中的分形边缘检测技术 ,提出了分形理论的裂缝检测方法 (多尺度分形参数的地毯覆盖方法和分形压缩方法 )。
补充资料：分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段，总长度变为 3×4／3＝4 英尺；每一次变换使总长度变为乘以4／3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。 计算分形维数的公式是 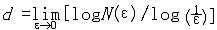 ，式中ε是小立方体一边的长度， N （ε）是用此小立方体覆盖被测形体所得的数目，维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ，覆盖一根单位 长度的线 段所需 的数目要 N （ε）＝1／ε2，覆盖一个单位边长的正方形，N(ε)＝（1／ε）2 ，覆盖单位边 长的立方体，N （ε）＝（1／ε）3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d＝1.2618，谢尔宾斯基海绵的维数d＝ 2.7268。对于无规分形，可用不同的近似方法予以计算，也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条