|
|
|
说明:双击或选中下面任意单词,将显示该词的音标、读音、翻译等;选中中文或多个词,将显示翻译。
|
|
|
1) rectangular parts optimal layout

矩形件优化排样
2) the rectangular cutting stock problem

矩形件排样优化
1.
To resolve the rectangular cutting stock problem,this paper proposes a new greedy algorithm,based on analyzing the main disadvantage of the traditional approximate algorithm.
针对矩形件排样优化问题,分析了传统近似算法的主要缺陷,在此基础上,提出一种新的排样算法——贪婪算法。
3) packing of rectangles

矩形排样优化
1.
The packing of rectangles is a NP-Complete problem and possesses widespread applications in the industry,such as the cutting of clothing,metal and composition of news.
矩形排样优化属于NPC问题,在工业界有着广泛的应用,如布料切割、金属下料和新闻组版等。
4) optimal packing of rectangles

形件优化排样
5) 2-D irregular-shaped cutting stock problem

异形件优化排样
6) rectangular strip packing problem

矩形件排样
1.
A discrete particle swarm algorithm for the rectangular strip packing problem is presented.
提出了一种基于离散粒子群优化算法求解矩形件排样问题的方法。
补充资料:一种钣金件结构强度计算和优化
用有限元法对新品进行强度计算和优化是提高设计质量、低成本的有效手段,而有效运用这种方法的先决条件是保证计算结果的正确性。本文通过对一种钣金零件的强度计算,着重探讨了“有限元”法中“边界条件”对计算结果的影响,特别是分析对象在工作环境中有“位移”的情况。 用“有限元法”对设计产品进行强度计算,并通过计算结果对设计产品进行优化改进是新产品研发过程中不可缺少的环节,随着CAD/CAE/CAM等技术的普及,这种方法在缩短新品开发周期及节约成本方面的作用更为凸显。“有限元法”的有效性不仅体现在有限元应用软件本身,更体现在对实际模型进行抽象、简化的过程及结果中,即分析模型的“边界条件”。本文对一种支架零件进行强度较核计算,在分析模型中对边界条件进行“微调”,最终得出近乎想象的分析结果,进一步例证和阐述了建立符合实际工况条件的“边界条件”的重要性。只有保证计算结果的正确性,才能通过优化程序对产品结构参数进行优化,以期得到满足工程要求的结果。 一、应用背景 建立分析对象的三维模型,如图1所示。 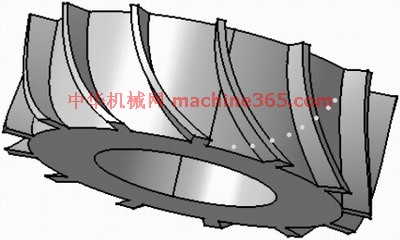
图1分析对象的三维模型 该零件是冲压成型的钣金件,是电冰箱上的支撑架,主要承受重力和搬运过程中的冲击力。由于零件壁厚均匀,因此零件的分析模型宜采用“壳”单元模型。 美国参数技术公司(PTC)的软件是优秀的高端MCAD设计软件之一,基于特征的全参数化及全相关技术极大地提高了设计效率和质量。其中,CAE专用分析模块 Pro/MECHANIC实现了与Pro/ENGINEER的完全无缝集成,由于Pro/MECHANIC采用高阶次单元(P单元),使分析模型的网格生成变得简单容易,无需对原模型结构进行大量的简化处理。Pro/MECHANICA实现了与其他PTC产品、数据管理工具及其他CAD工具的真正交互性。参数化优化结合了Pro/ENGINEER的全部功能后,Pro/MECHANICA可以提供真正的参数化分析,使用相关仿真特征,因为与后续产品(模具、刀路轨迹等)完全相关,即使设计更改后,也不需要重新定义分析。 该零件的三维模型是用Pro/ENGINEER 软件完成的,强度计算在Pro/ENGINEER与Pro/MECHANIC的集成环境中进行,计算用Pro/MECHANIC解算器。 二、分析模型的建立
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|




