1) Grassmann line geometry
Grassmann线几何
2) geometric midline
几何中线
1.
The geometric midlines of error triangles or gaps between Tresca and Twin shear stress yield loci on π -plane were linked up together to form a third yield locus which reflects a new yield criterion called GM(geometric midline) yield criterion in Haigh Westergaard stress space.
在π平面上,取Tresca屈服轨迹与双剪应力屈服轨迹之间误差三角形的几何中线确定新的屈服轨迹,建立了该轨迹在HaighWestergaard应力空间上的应力方程,称此方程为几何中线屈服方程或简称GM屈服准则·证明了单位塑性功率表达式及其对Mises圆的逼近精度·精度分析与算例表明该准则与Mises准则的最大误差不超过2 9%,平均误差仅为0 95%,比MY(平均屈服)准则的逼近精度提高1%,且它是线性的,其轨迹为与Mises屈服轨迹相交的等边非等角十二边形·该准则的单位体积塑性功率表达式也是线性的
3) geometric linear
几何线性
4) epipolar geometry
极线几何
1.
Stereo matching on uncalibrated images based on epipolar geometry;
基于极线几何约束的非标定图像的立体匹配
2.
Improved multi-constrained image stereo matching based on epipolar geometry
基于极线几何的改进多约束图像立体匹配
3.
The expected area was generated based on the fundamental matrix, an important concept of epipolar geometry.
该方法根据极线几何理论,利用基本矩阵离线地得到故障诊断的期望范围,再根据匹配像素点是否落在期望范围内判断视觉模块当前是否存在故障。
5) geometric route
几何线形
1.
Kinematics appraisal on the geometric route of high-speed loop;
高速环道几何线形的运动学评价
6) geometrical ray
几何光线
补充资料：画法几何:截交线
截交线
平面与空间形体表面的交线。它是画法几何研究的内容之一。当空间形体表面是曲面时﹐截交线是一条平面曲线﹐当空间形体表面由若干个平面组成时﹐截交线是一个多边形。在给定平面和空间形体的相对位置后﹐从多面正投影图中可以容易地画出平面和空间形体的投影﹐但它们截交线的投影一般不能直接画出﹐通常需要採用辅助面法先求出截交线上若干点的投影﹐然后再将它们连接成截交线。例如图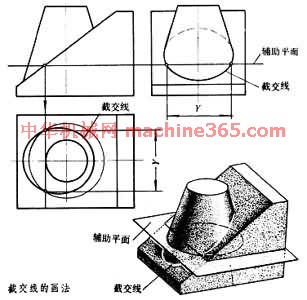
截交线的画法 中圆锥台和空间形体上的斜面相交﹐须用辅助面法求取截交线上的点。辅助面法是先选取某个面作为辅助面(图 截交线的画法
中是水平面)﹐然后作出辅助面和斜面的交线﹑辅助面和圆锥的交线。图 截交线的画法
中这两条交线分别是直线和圆。最后作出两交线的交点。所得到的交点就是截交线上的点。改变辅助面的位置﹐重复上述作图过程﹐则能获得足够数量的点﹐连接成截交线。运用辅助面法的关键在於选择合适的辅助面﹐辅助面和空间形体的交线投影应是直线或者是圆。当空间形体的表面为平面时﹐其截交线是多边形﹐只须用辅助面法求出多边形的各顶点即可连成截交线。
平面与空间形体表面的交线。它是画法几何研究的内容之一。当空间形体表面是曲面时﹐截交线是一条平面曲线﹐当空间形体表面由若干个平面组成时﹐截交线是一个多边形。在给定平面和空间形体的相对位置后﹐从多面正投影图中可以容易地画出平面和空间形体的投影﹐但它们截交线的投影一般不能直接画出﹐通常需要採用辅助面法先求出截交线上若干点的投影﹐然后再将它们连接成截交线。例如图
截交线的画法 中圆锥台和空间形体上的斜面相交﹐须用辅助面法求取截交线上的点。辅助面法是先选取某个面作为辅助面(图 截交线的画法 中是水平面)﹐然后作出辅助面和斜面的交线﹑辅助面和圆锥的交线。图 截交线的画法 中这两条交线分别是直线和圆。最后作出两交线的交点。所得到的交点就是截交线上的点。改变辅助面的位置﹐重复上述作图过程﹐则能获得足够数量的点﹐连接成截交线。运用辅助面法的关键在於选择合适的辅助面﹐辅助面和空间形体的交线投影应是直线或者是圆。当空间形体的表面为平面时﹐其截交线是多边形﹐只须用辅助面法求出多边形的各顶点即可连成截交线。说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条