1) hyperbolic parabolic equation


双曲型热传导方程
1.
In this paper,we consider the numerical simulations of two kinds of equations: One is the Sobolev equation, and the other is the hyperbolic parabolic equation.
本文利用H~1-Galerkin混合有限元方法讨论了两类问题一抛物型Sobolev方程初边值问题和双曲型热传导方程初边值问题的数值模拟。
2) double-temperature heat conduction equation


双温热传导方程
1.
This paper proposes a new kind of two-level implicit weighted optimal difference scheme with parameters for the double-temperature heat conduction equation U_t+U_x+U_(xx)-δU_(xxt)=0(δ>0).
提出了一个解双温热传导方程Ut+Ux +Ux x -δUx xt=0 (δ>0 )的一种新的具有二阶精度的两层加权隐格式,其截断误差阶为o(τ2 +h2 ) ,此格式是条件稳定的,特别是当θ=12 时,此格式绝对稳定。
3) Hyperbolic heat conduction model


双曲线热传导模型
4) hyperbolic heat conduction


双曲型导热
1.
The influence of volumetric absorption on the hyperbolic heat conduction in laser-irradiated tissue was studied by combining the seven-flux model of light propagation with the two-dimensional hyperbolic heat conduction model in cylindrical coordinates.
将激光传输的七流模型与圆柱坐标系内二维双曲型导热方程相结合,讨论了激光容积吸收对生物组织内双曲型导热过程的影响。
2.
Considering the laser applications in biology and medicine as background, this paper presented a theoretical research on the hyperbolic heat conduction in laser irradiated tissue.
以激光在生物医学中的应用为背景 ,对激光照射下生物组织内的双曲型导热问题进行了研究。
5) dual-phase-lagging heat conduction equations


双相滞热传导方程
1.
This paper is concerned with the mixed boundary problems of dual-phase-lagging heat conduction equations arising in many fields.
本文考虑一类具有广泛应用背景的双相滞热传导方程混合边界问题。
6) Heat-conduction equation


热传导方程
1.
A stefan problem of Heat-conduction equations with heat source;


一类含热源的热传导方程Stefan问题
2.
An ADI scheme for solving heat-conduction equation of high-dimension;


解高维热传导方程的一个高精度ADI格式
3.
In this paper,the exact solution and approximate solution of the boundary control problem for a class of the heat-conduction equation are given.
给出了热传导方程边界控制问题的精确解和近似解,证明了近似解对精确解的收敛性。
补充资料:热传导方程
| 热传导方程 heat conduction,equation of 最早在研究热的传导问题时得到的方程。它的一维形式是 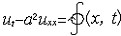 ,其中u为温度函数, ,其中u为温度函数,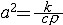 ,k为热传导系数,c是比热容,ρ是密度, ,k为热传导系数,c是比热容,ρ是密度,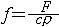 是外热源密度。热传导方程也可以描述其他物理现象,比如扩散过程等等。方程连同初始条件及(或)边界条件的任一种,都可组成初值问题、边值问题或初边值问题。 是外热源密度。热传导方程也可以描述其他物理现象,比如扩散过程等等。方程连同初始条件及(或)边界条件的任一种,都可组成初值问题、边值问题或初边值问题。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条