1) the fixed solutions of one dimensional equations of heat transfer


一维热传导方程的定解
2) One Dimensional Heat Equation


一维热传导方程
1.
The Semi-discrete Finite Difference Method for Solving One Dimensional Heat Equation;


求解一维热传导方程的一种半离散差分格式
4) 4-D heat equation


四维热传导方程
1.
A class of two-level explicit difference schemes for solving 4-D heat equation are presented, when the order of trunction error is O(△t +△x2), the stability condition is the mash ratio r =△t/△x2 =△t/△y2 =△t/△z2 =△t /△w2≤11/24, which is better than that of all other explicit difference schemes.
构造了解四维热传导方程的一族两层显格式,证明了当截断误差为O(△t+△x2)时,其稳定性条件为网比r=△t/△x2=△t/△y2=△t/△z2=△t/△w2≤11/24优于同类的其他显格式,当截断误差阶为O(△t2+△x4)时,此格式为一个简洁而实用的高精度两层显格式。
5) two-dimensional heat-conduction equation


二维热传导方程
1.
The implicit difference scheme for two-dimensional heat-conduction equation is presented.


给出了二维热传导方程隐式差分格式。
6) three_dimensional heat conduction equation


三维热传导方程
1.
A class of two_level explicit difference schemes are presented for solving three_dimensional heat conduction equation.
提出了一族三维热传导方程的两层显式差分格式 ,当截断误差阶为O(Δt +(Δx) 2 )时 ,稳定性条件为网格比r=Δt(Δx) 2 =Δt(Δy) 2 =Δt(Δz) 2 ≤ 12 ,优于其他显式差分格式· 而当截断误差阶为O((Δt) 2 +(Δx) 4 )时 ,稳定性条件为r≤ 1/ 6 ,包含了已有的结果
补充资料:热传导方程
| 热传导方程 heat conduction,equation of 最早在研究热的传导问题时得到的方程。它的一维形式是 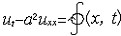 ,其中u为温度函数, ,其中u为温度函数,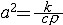 ,k为热传导系数,c是比热容,ρ是密度, ,k为热传导系数,c是比热容,ρ是密度,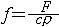 是外热源密度。热传导方程也可以描述其他物理现象,比如扩散过程等等。方程连同初始条件及(或)边界条件的任一种,都可组成初值问题、边值问题或初边值问题。 是外热源密度。热传导方程也可以描述其他物理现象,比如扩散过程等等。方程连同初始条件及(或)边界条件的任一种,都可组成初值问题、边值问题或初边值问题。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条