1) harmonic vibration compound


简谐振动的合成
1.
The designing methods,functions and applications of CAI courseware are introduced in this article based on the example of using VB produce CAI courseware on harmonic vibration compound.
本文结合在大学物理教学中,研究制作简谐振动合成的CAI课件的过程,比较几种常用的开发课件的方法及优缺点,以用VB制作简谐振动的合成的CAI课件为例,介绍课件的制作方法,课件的功能及应用情况。
3) simple harmonic oscillation


简谐振动
1.
DIS exploring experiment of simple harmonic oscillation


水平方向简谐振动的DIS实验
2.
Based on theory of simple harmonic oscillation in physics,this paper presents a novel model for production decline prediction given by deformation of critical damping oscillation equation which is predigest.
基于物理学中的简谐振动原理,提出了把阻尼振动方程中的临界阻尼振动方程变形得到一种新的产量递减模型,可简化为Arps指数递减形式,经实例计算,可以用来预测油田产量,以此指导油田开发和管理。
3.
This paper presents a simple method for measuring gas adiabatic constant by use of simple harmonic oscillation.
本文介绍了一种简单的利用简谐振动现象测量气体的定熵指数的方法。
4) Harmonic vibration


简谐振动
1.
Describe harmonic vibration with rotation vector;


用旋转矢量描述简谐振动
2.
Application of rotation vector on phase of harmonic vibration


旋转矢量法在简谐振动教学中的应用
3.
During the teaching of Medical Physics, it is difficult to describe harmonic vibration with rotation vector clearly just with some static pictures.
《医学物理学》课程中,简谐振动旋转矢量法的学习,仅靠静态图片不利于阐明其原理。
5) simple harmonic vibration


简谐振动
1.
The Rheovibron measures the damping of material according to the longitudinal simple harmonic vibration of equal cross section bar.
流变振动仪利用等截面杆的纵向简谐振动来测定材料的阻尼,十分方便和有效。
2.
The important parameters, which characterize the Lissajous’ figures, are presented by synthesizing two mutually vertical simple harmonic vibrations whose ratio of frequencies is a rational number.
通过对两个相互垂直、频率比为有理数的简谐振动的合成研究,提出了描述合振动轨迹的特征参量:振幅比、频率比、图形余弦、方向正弦。
3.
Dynamic equation of simple harmonic vibration machine with Single-degree-of-freedom is solved by transfer function algorithm,accordingly,obtains relationship between displacement of vibration body and exciting force.
采用传递函数法求解单自由度简谐振动机械的动力学方程,得到振动体位移与激振力的关系,通过激振力频率和振动体质量的波动对振动体振幅的影响分析,以及隔振系数与频率比关系的分析,提出了该类振动机械合理的下限频率比;同时考虑到弹性支承在振动体重力作用下的静变形应大于振动体的最大振幅,从而给出了弹性支承刚度的设计依据和激振力幅值的计算公式,为单自由度简谐振动机械的设计提供了系统的理论和方法,并通过算例进一步阐述了该设计方法的应用。
6) simple harmonic motion


简谐振动
1.
The modification for the metrical formula of simple harmonic motion cycle;


对气轨上简谐振动周期测量公式的修正
2.
Demonstrating simple harmonic motion byreference circle method;


用参考圆法演示简谐振动
3.
Derivation of Simple Harmonic Motion Equation;


简谐振动运动方程的推导
补充资料:简谐振动
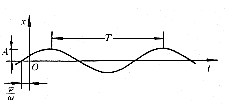
| 简谐振动 simple harmonic vibration 描述系统状态的物理量随时间按正弦或余弦规律作周期性变化的过程。又称简谐运动。作简谐振动的物体的加速度始终同它的位移成正比,但方向相反。即x=-ω2x, 式中ω2为比例常量。作简谐运动的物体,其运动规律可表达为: x=Asin(ωt+ 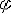 ) )=Asin(2πt/T+ 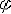 ) )=Asin(2πf t+ 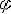 ) )式中x为位移;A为振幅;ω为角(圆)频率;t为时间;T为周期;f 为频率;ωt+ 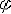 为相位 ; 为相位 ;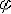 为初相位(见图)。这种运动对其平衡位置(零点)是对称的。在零点上,物体速度最大,加速度为零;在最大位移处(转向点),速度为零,加速度最大。简谐运动是最简单、最基本的振动形式;任何周期振动都可由许多不同频率和振幅的简谐运动合成。简谐运动是单自由度无阻尼系统微幅自由振动的抽象模型。悬挂在弹簧下端物体的微幅振动,扭摆的微幅振动以及晶体中原子围绕平衡位置的微幅振动都可近似地看作简谐振动。 为初相位(见图)。这种运动对其平衡位置(零点)是对称的。在零点上,物体速度最大,加速度为零;在最大位移处(转向点),速度为零,加速度最大。简谐运动是最简单、最基本的振动形式;任何周期振动都可由许多不同频率和振幅的简谐运动合成。简谐运动是单自由度无阻尼系统微幅自由振动的抽象模型。悬挂在弹簧下端物体的微幅振动,扭摆的微幅振动以及晶体中原子围绕平衡位置的微幅振动都可近似地看作简谐振动。
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条