1) fuzzy integral transformation


Fuzzy 积分变换
1.
In this paper one kind of the fuzzy integral transformation is given to discuss some its properies and applica-tions to the fuzzy set,the Sugeno integral and a matric for the Fuzzy number set.
本文提出了一种Fuzzy 积分变换,讨论了它的若干性质和在Fuzzy 集、S-型积分、Fuzzy 数的度量中的应用。
2) S-fuzzy integral-transformation


S型Fuzzy积分变换
1.
The S-fuzzy integral-transformation was suggested in [3],in the meantime, its some properties and applications were studied.
文献[3]提出了S型Fuzzy积分变换,并研究了它的一些性质及其应用,本文是在文[3]的基础上,在非负递减函数空间上引进距离的概念,从而获得这种Fuzzy积分变换和Sugeno意义下的S型Fuzzy积分关于这种距离是一致连续的结果。
3) fuzzy integral


Fuzzy积分
1.
Discussion on introducing Fuzzy integral evaluation system in teaching quality of physical educaion courses in general colleges and universities;
高校体育课程教学质量引入Fuzzy积分评估系统的探讨
2.
Discussing the common evaluation models and the structure of fuzzy integral,we point out the association between fuzzy synthetic evaluation and pan-integral of which the convergence theorem can play well a basic role in association.
通过对常见的评判模型的讨论以及对Fuzzy积分结构的探讨,指出了泛积分与Fuzzy综合评判之间的联系,而泛积分在一定条件下的收敛定理为此打下了良好的基础。
3.
Based on actual situation in Songshan District, combining with characteristics of measures of prevention and combat, by use of comprehensive judgment model with Fuzzy integral, the method of raking tree artificially to preventing and combating Dendrolimus can be utilized intensively because of its low cost and less influence by climate and forest land.
本文根据松山区实际情况 ,综合各防治措施特征 ,应用 Fuzzy积分构造的综合评判模型 ,选择了人工搂树盘防治松毛虫危害措施 ,相对比成本低、可操作性强 ,气象、林地条件等障碍因素少 ,被广泛应
4) fuzzy pan-integral


Fuzzy泛积分
1.
Based on the concepts of pan-integral defined in fuzzy measure space and fuzzy pan-integral on fuzzy sets, the transformation theorems are set up.
基于Fuzzy测度空间上的泛积分和定义在Fuzzy集合上的泛积分概念,建立了Fuzzy泛积分转化定理,它揭示了Fuzzy集合上Fuzzy泛积分与经典集合上泛积分之间的关系,使得Fuzzy集合上的Fuzzy泛积分问题可以转化到经典集合上去讨论,从而可以很容易地证明,定义在经典集合上的泛积分的许多相关结论在Fuzzy泛积分中仍然成立·转化定理Ⅰ建立了从一般的Fuzzy泛空间到经典Fuzzy泛空间的转化定理;转化定理Ⅱ建立了从一般的Fuzzy泛空间到正实数集中Borel集引出的Fuzzy泛空间的转化定理
5) L-fuzzy integration


L-Fuzzy积分
6) complex fuzzy integral


复Fuzzy积分
补充资料:积分变换
| 积分变换 integral transform 通过参变量积分将一个已知函数变为另一个函数。已给f(x),如果 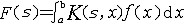 存在(a、b可为无穷),则称F(s)为f(x)以K(s,x)为核的积分变换。 存在(a、b可为无穷),则称F(s)为f(x)以K(s,x)为核的积分变换。积分变换无论在数学理论或其应用中都是一种非常有用的工具。最重要的积分变换有傅里叶变换、拉普拉斯变换。由于不同应用的需要,还有其他一些积分变换,其中应用较为广泛的有梅林变换和汉克尔变换,它们都可通过傅里叶变换或拉普拉斯变换转化而来。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条