1) dynamical Pauli effect


动力学泡利效应
2) kinetic effect


动力学效应
1.
The glass transition temperature, Tg, the onset crystallization temperature, Tx, and the crystallization peak temperature, Tpi, of the BMG are found to depend on the heating rate during the continuous heating, suggesting that both glass transition and crystallization have a significant kinetic effect.
实验表明,在 Zr基大块非晶合金中掺入 Fe后,其玻璃转变与晶化行为都与加热速率有关,均具有动力学效应。
3) Dynamic Effect


动力学效应
1.
The influence of temperature and pressure on diamond which is synthesized using powder technology is investigated and its dynamic effect i s discussed, enhancing understanding of characteristics of diamond synthesis.
考查了合成温度、压力对粉末工艺金刚石合成的影响 ,探讨了其动力学效应 ,加深了对粉末工艺金刚石合成特性的认识。
2.
A study on dynamic effect of three point bending beam made of laminated composite subjected totransverse impact have been carried out.
研究了十字叠层复合材料梁横向冲击响应的动力学效应,根据冲击实验曲线用动态有限元方法计算了惯性效应和应力波效应对位移和应力响应的影响。
4) Dynamics effect


动力学效应
1.
Compound modification function and dynamics effect of low - Cr white cast iron;


低铬白口铸铁复合变质的作用及动力学效应
6) kinetic compensation effect


动力学补偿效应
1.
The decomposition processes and kinetic parameters of RDX and HMX are markedly affected by test conditions, specimen state and test method, and the "kinetic compensation effect"and "isokinetic points(temperatures)" exist in these parameters.
RDX和HMX在不同的分解阶段有不同的动力学参数和机理函数,其分解过程和动力学参数受试验条件、样品状态和试验方法的影响很大,但这些参数之间存在"动力学补偿效应"和"等动力学点"。
2.
The matching of one set of experimental data with several pyrolysis models is explained in terms of kinetic compensation effect.
阐述了目前被许多研究者所运用的模型匹配方法求解动力学参数的不足之处,并从动力学补偿效应的角度来说明一组实验数据可以与多个模型匹配的情况。
3.
92 min-1,and the kinetic compensation effect equation of ln A=0.


92 min-1,动力学补偿效应方程为lnA=0。
补充资料:泡利
| 泡利(1900~1958) Pauli,Wolfgang Ernst 瑞士籍奥地利物理学家。1900年4月25日生于维也纳,1958年12月15日卒于苏黎世 。1918年中学毕业后就成为慕尼黑大学的研究生 ,1921年获博士学位后,赴格丁根大学随M.玻恩研究一学期,再赴哥本哈根大学随A.N.玻尔一年。1940年任普林斯顿高级研究院的理论物理访问教授。 1921年 ,泡利20岁时为《数学科学百科全书》写相对论,此书在数学界具权威性。1924年提出说明电子能态的第四个量子数其数值可取作 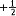 或 或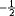 。后来发现,这两个数值代表费米子自旋的两种可能取向。1925年发现不相容原理(今称泡利不相容原理),即一个原子内不能有一个以上电子具有相同的状态。这个原理把量子论和观察到的原子特性联系起来 。为此获1945年诺贝尔物理学奖。在20世纪20年代后期观察到,当一个原子核发射出一个β粒子(电子)时,总有一些能量和动量丧失掉 ,这就违反了守恒律 。泡利在1930年提出,丧失掉的能量和动量是被某种中性粒子(后来由E.费米命名为中微子)从核里带走了。此外,泡利对量子场论也有重大贡献。 。后来发现,这两个数值代表费米子自旋的两种可能取向。1925年发现不相容原理(今称泡利不相容原理),即一个原子内不能有一个以上电子具有相同的状态。这个原理把量子论和观察到的原子特性联系起来 。为此获1945年诺贝尔物理学奖。在20世纪20年代后期观察到,当一个原子核发射出一个β粒子(电子)时,总有一些能量和动量丧失掉 ,这就违反了守恒律 。泡利在1930年提出,丧失掉的能量和动量是被某种中性粒子(后来由E.费米命名为中微子)从核里带走了。此外,泡利对量子场论也有重大贡献。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条