1) Schrodinger equation of higher order
高阶薛丁谔方程
2) higher-order nonlinear Schrodinger equation
高阶非线性薛定谔方程
1.
By using the fractional transformation method, the exact solutions of the higher-order nonlinear Schrodinger equation are obtained which included Jacobian elliptic function solution and new solitary wave solution.
本文基于分数变换原理,研究了用于描述飞秒光脉冲传输的高阶非线性薛定谔方程,得到了它的各种包络型Jacobian椭圆函数双周期解和新型亮孤波解。
3) schrdinger equation of higher order
高阶薛丁锷方程
4) Coupled higher-order nonlinear Schrdinger equations
耦合高阶非线性薛定谔方程
1.
Coupled higher-order nonlinear Schrdinger equations (CHNLS),governing the evolution of two orthogonal polarization components of ultrashort optical pulse in birefringent fiber,are derived from the dispersion relation.
从色散关系出发 ,推导了描述超短光脉冲不同偏振分量在双折射光纤中传输特性的耦合高阶非线性薛定谔方程 (CHNLS) ,在一定参量下得到了亮亮、暗暗、亮暗孤波解析解 ,包括一种非常特殊的“W”型孤波解 ,并对这些孤波解的特性进行了分
5) The (higher-order) nonlinear Schr(o|¨)dinger equation with variable coefficients
变系数(高阶)非线性薛定谔方程
补充资料：薛定谔方程
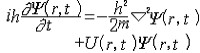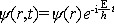薛定谔方程 E.薛定谔提出的量子力学基本方程 。建立于 1926年。它是一个非相对论的波动方程。它反映了描述微观粒子的状态随时间变化的规律，它在量子力学中的地位相当于牛顿定律对于经典力学一样，是量子力学的基本假设之一。设描述微观粒子状态的波函数为Ψ（r，t），质量为m的微观粒子在势场U（r，t）中运动的薛定谔方程为  。在给定初始条件和边界条件以及波函数所满足的单值、有限、连续的条件下，可解出波函数Ψ（r，t）。由此可计算粒子的分布概率和任何可能实验的平均值（期望值）。当势函数U不依赖于时间t时，粒子具有确定的能量，粒子的状态称为定态。定态时的波函数可写成 式中Ψ（r）称为定态波函数，满足定态薛定谔方程 ，这一方程在数学上称为本征方程，式中E为本征值，是定态能量，Ψ（r）又称为属于本征值E的本征函数。量子力学中求解粒子问题常归结为解薛定谔方程或定态薛定谔方程。薛定谔方程广泛地用于原子物理、核物理和固体物理，对于原子、分子、核、固体等一系列问题中求解的结果都与实际符合得很好。 薛定谔方程仅适用于速度不太大的非相对论粒子，其中也没有包含关于粒子自旋的描述。当计及相对论效应时，薛定谔方程由相对论量子力学方程所取代，其中自然包含了粒子的自旋。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条