1) particle for instantaneous velocity center


瞬心质点
1.
This paper discusses how to apply the theorem of moment of momentum about the particle for instantaneous velocity center to derive the differential equation of ro-tation of a rigid body about the instantaneous velocity center.
讨论了如何正确应用对瞬心质点的动量矩定理推导刚体绕瞬时速度中心的转动微分方程。
2) instantaneous centre of the velocity


速度瞬心点
3) instantaneoussound particle displacement


瞬时声质点位移
4) instantaneoussound particle velocity


瞬时声质点速度
5) ε-centroid


ε质心点
6) centroids of firepoints


火点质心
补充资料:机械原理:瞬心
瞬心刚体或机构中的构件作平面运动时的瞬时迴转中心。其中瞬时速度为零的﹐称为绝对瞬心﹔当一刚体对另一刚体作相对平行平面运动时﹐其瞬时相对速度为零﹐瞬时绝对速度相同的重合点称为相对瞬心。因此﹐绝对瞬心也可看作是运动刚体相对於固定刚体的相对瞬心。相对瞬心和绝对瞬心都指速度瞬心﹐瞬心是速度瞬心的简称。当机构的构件较少时﹐用瞬心来分析机构的速度比较简单清楚。瞬时加速度为零的点称为加速度瞬心。
瞬心的求法 平面机构中任意两个构件有一个瞬心(图1 瞬心的求法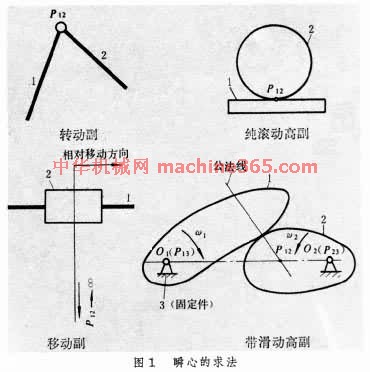 )。转动副的瞬心在相对转动中心。移动副的瞬心在相对移动垂直方向的无限远处。纯滚动高副机构的瞬心在两构件的接触点。带滑动高副机构的瞬心在过两构件接触点的公法线上﹐其具体位置可由三心定理求得﹕在平行平面中作确定相对运动的3个构件共有3个相对瞬心﹐它们都位於同一直线上。用观察方法不能求得的其他瞬心也只能用三心定理来求取。利用瞬心是两构件速度相同的重合点这一概念可得出﹕两构件 1﹑2的传动比﹐与其被轮廓接触点的公法线所分割的连心线的两线段长度成反比﹐即 w1/ w2=P 12O 2/P 12O 1。瞬心求法不适用於较复杂的机构﹐对某些机构要求出其全部瞬心也比较困难。
)。转动副的瞬心在相对转动中心。移动副的瞬心在相对移动垂直方向的无限远处。纯滚动高副机构的瞬心在两构件的接触点。带滑动高副机构的瞬心在过两构件接触点的公法线上﹐其具体位置可由三心定理求得﹕在平行平面中作确定相对运动的3个构件共有3个相对瞬心﹐它们都位於同一直线上。用观察方法不能求得的其他瞬心也只能用三心定理来求取。利用瞬心是两构件速度相同的重合点这一概念可得出﹕两构件 1﹑2的传动比﹐与其被轮廓接触点的公法线所分割的连心线的两线段长度成反比﹐即 w1/ w2=P 12O 2/P 12O 1。瞬心求法不适用於较复杂的机构﹐对某些机构要求出其全部瞬心也比较困难。
瞬心线和瞬心线机构 两个作确定相对运动的构件在每一瞬时都有一个瞬心﹐分别将这两个构件上所有作过瞬心的各点连成曲线即得到两条瞬心线。将这两条瞬心线作成相互滚动的轮廓线以传递运动的机构﹐称为瞬心线机构。这种机构能重演这两个构件的确定相对运动。例如带滑动高副机构﹐其构件1﹑2的两条轮廓曲线接触点在传动过程中存在滑动﹐故它们是一对共軛曲线。求出其在不同接触位置的瞬心P 12﹐就不难求得与这对共軛曲线相应的一对瞬心线。用这对瞬心线作轮廓线的机构﹐可以代替相应的共軛曲线机构。如果P 12在连心线上的位置不变﹐则构件1﹑2的传动比为常数﹐而瞬心线也就成为两段圆弧。若两条相互滚动的瞬心线为两个椭圆﹐就成为椭圆瞬心线机构(图2 椭圆瞬心线机构 )。
椭圆瞬心线机构 )。
瞬心的求法 平面机构中任意两个构件有一个瞬心(图1 瞬心的求法
 )。转动副的瞬心在相对转动中心。移动副的瞬心在相对移动垂直方向的无限远处。纯滚动高副机构的瞬心在两构件的接触点。带滑动高副机构的瞬心在过两构件接触点的公法线上﹐其具体位置可由三心定理求得﹕在平行平面中作确定相对运动的3个构件共有3个相对瞬心﹐它们都位於同一直线上。用观察方法不能求得的其他瞬心也只能用三心定理来求取。利用瞬心是两构件速度相同的重合点这一概念可得出﹕两构件 1﹑2的传动比﹐与其被轮廓接触点的公法线所分割的连心线的两线段长度成反比﹐即 w1/ w2=P 12O 2/P 12O 1。瞬心求法不适用於较复杂的机构﹐对某些机构要求出其全部瞬心也比较困难。
)。转动副的瞬心在相对转动中心。移动副的瞬心在相对移动垂直方向的无限远处。纯滚动高副机构的瞬心在两构件的接触点。带滑动高副机构的瞬心在过两构件接触点的公法线上﹐其具体位置可由三心定理求得﹕在平行平面中作确定相对运动的3个构件共有3个相对瞬心﹐它们都位於同一直线上。用观察方法不能求得的其他瞬心也只能用三心定理来求取。利用瞬心是两构件速度相同的重合点这一概念可得出﹕两构件 1﹑2的传动比﹐与其被轮廓接触点的公法线所分割的连心线的两线段长度成反比﹐即 w1/ w2=P 12O 2/P 12O 1。瞬心求法不适用於较复杂的机构﹐对某些机构要求出其全部瞬心也比较困难。 瞬心线和瞬心线机构 两个作确定相对运动的构件在每一瞬时都有一个瞬心﹐分别将这两个构件上所有作过瞬心的各点连成曲线即得到两条瞬心线。将这两条瞬心线作成相互滚动的轮廓线以传递运动的机构﹐称为瞬心线机构。这种机构能重演这两个构件的确定相对运动。例如带滑动高副机构﹐其构件1﹑2的两条轮廓曲线接触点在传动过程中存在滑动﹐故它们是一对共軛曲线。求出其在不同接触位置的瞬心P 12﹐就不难求得与这对共軛曲线相应的一对瞬心线。用这对瞬心线作轮廓线的机构﹐可以代替相应的共軛曲线机构。如果P 12在连心线上的位置不变﹐则构件1﹑2的传动比为常数﹐而瞬心线也就成为两段圆弧。若两条相互滚动的瞬心线为两个椭圆﹐就成为椭圆瞬心线机构(图2
 椭圆瞬心线机构 )。
椭圆瞬心线机构 )。说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条