1) 0digonally quasiconcave relation


0-对角拟凹关系
2) 0-diagonally quasi-concave (quasiconvex)


0-对角拟凹(拟凸)
3) 0-diagonallyconcave


0-对角凹
4) 0-diagonally convex relation


0-对角凸关系
5) diagonal quasiconcavity


对角拟凹
1.
In this paper, we first introduce some notions about diagonal transfer continuity, diagonal quasiconcavity and FS-convexity, then obtain new existence theorems of Nash equilibria deduced from KKM lemma in non-compact sets.
引进对角转移连续,对角拟凹和FS-凸等概念,然后在非紧的策略集上运用KKM引理得到新的Nash平衡存在性结果。
6) γ-digonally quasiconcave


γ-对角拟凹
补充资料:--关系
 -
- -
- guanxi
guanxi -
- -
- 关系
关系p-V-T relation
物质在平衡状态下压力(
 )-体积(
)-体积( )-温度(
)-温度( )之间的相互关系的简称。这三个变量之间存在一定的关系,如物质体积的热胀冷缩和随压力增加而减小,这都是人们所共知的现象。在化工热力学中,需要对各种物质特别是对流体(气体和液体的统称)的
)之间的相互关系的简称。这三个变量之间存在一定的关系,如物质体积的热胀冷缩和随压力增加而减小,这都是人们所共知的现象。在化工热力学中,需要对各种物质特别是对流体(气体和液体的统称)的 -
- -
- 关系进行定量研究。其目的之一是直接利用
关系进行定量研究。其目的之一是直接利用 -
- -
- 数据,对已知温度、压力的流体作质量与体积的互算,进而用于计算流体的流量、输送管道、反应器等的几何尺寸。其目的之二是利用
数据,对已知温度、压力的流体作质量与体积的互算,进而用于计算流体的流量、输送管道、反应器等的几何尺寸。其目的之二是利用 -
- -
- 关系计算某些不能直接测定的热力学性质如焓、熵、逸度等,进而作热力学过程的热功计算或相平衡计算、化学平衡计算。一定量纯物质的
关系计算某些不能直接测定的热力学性质如焓、熵、逸度等,进而作热力学过程的热功计算或相平衡计算、化学平衡计算。一定量纯物质的 -
- -
- 关系常在三维直角坐标系中表示,称作
关系常在三维直角坐标系中表示,称作 -
- -
- 关系立体图。
关系立体图。典型
 -
- -
- 关系立体图 [kg2]
关系立体图 [kg2] 一定量纯物质在平衡状态下的
一定量纯物质在平衡状态下的 -
- -
- 关系,在以
关系,在以 、
、
 (摩尔体积)和
(摩尔体积)和 为坐标轴的空间形成曲面(图1[典型
为坐标轴的空间形成曲面(图1[典型 -
- -
- 关系立体图]
关系立体图]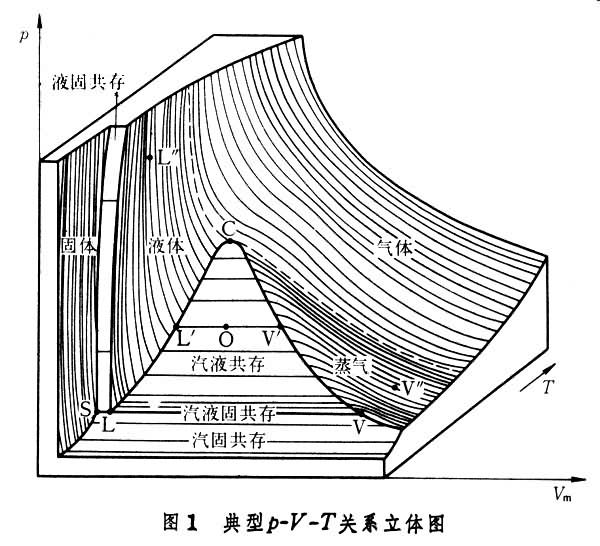 -
- -
- 关系立体图" class=image>),它表明在
关系立体图" class=image>),它表明在 、
、
 、
、 三个变量中确定了任何两个变量之后,第三个变量即可随之确定,并可从图中曲面读出其数值。曲面的不同部位可以表示不同的相,包括单相或两相共存,甚至三相共存。当物质的
三个变量中确定了任何两个变量之后,第三个变量即可随之确定,并可从图中曲面读出其数值。曲面的不同部位可以表示不同的相,包括单相或两相共存,甚至三相共存。当物质的 、
、
 、
、 数值落在单相区时,系统中只能存在一个相(气相、液相或固相);当
数值落在单相区时,系统中只能存在一个相(气相、液相或固相);当 、
、
 [kg2]
[kg2] 、
、 数值落中两相区时,系统就为两相(汽液、汽固或液固)共存;当物质的
数值落中两相区时,系统就为两相(汽液、汽固或液固)共存;当物质的 、
、
 、
、 [kg2]
[kg2] 数值恰好落在三相共存线上时,系统就为汽液固三相共存。
数值恰好落在三相共存线上时,系统就为汽液固三相共存。图中的LCV是汽液共存面。通过此面的O点,作等温面或等压面与LCV面相交于L
 OV
OV 线,L
线,L 和V
和V 分别代表平衡时的液相和汽相。两相的温度、压力与 O点相同,但摩尔体积不等。液相摩尔体积小,汽相摩尔体积大。汽相与液相的相对量则取决于O点的具体位置,O点越接近L
分别代表平衡时的液相和汽相。两相的温度、压力与 O点相同,但摩尔体积不等。液相摩尔体积小,汽相摩尔体积大。汽相与液相的相对量则取决于O点的具体位置,O点越接近L 点,液相量越多。随温度升高,汽液共存线趋短,结束于C点,此点称为临界点。在此点,汽相与液相的差别消失。温度高于C点之值时,不可能再出现象LCV面上所代表的那种汽液两相共存的状态。 C点所在位置的压力、体积和温度,[kg2]
点,液相量越多。随温度升高,汽液共存线趋短,结束于C点,此点称为临界点。在此点,汽相与液相的差别消失。温度高于C点之值时,不可能再出现象LCV面上所代表的那种汽液两相共存的状态。 C点所在位置的压力、体积和温度,[kg2] 分别称为临界压力
分别称为临界压力
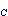 、临界体积
、临界体积
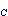 和临界温度
和临界温度
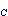 。在临界点上,[kg2]
。在临界点上,[kg2]
 对
对 的一阶偏导数和二阶偏导数均为零,[kg2]
的一阶偏导数和二阶偏导数均为零,[kg2] 即[496-01]
即[496-01] 。当温度低于临界温度时,流体(如V
。当温度低于临界温度时,流体(如V 点)被等温加压后,便经过V
点)被等温加压后,便经过V L
L 转变为液体(如L
转变为液体(如L 点);当温度高于临界温度时,流体经等温加压,就不可能出现液化现象。因此,将低于临界温度的流体称为蒸气,简称汽,将高于临界温度的流体称为气体或超临界流体(常指压力较高时的气体,它具有较大的分子扩散系数和密度,以及较小的粘度)。三个两相共存面相交于SLV线,[kg2]
点);当温度高于临界温度时,流体经等温加压,就不可能出现液化现象。因此,将低于临界温度的流体称为蒸气,简称汽,将高于临界温度的流体称为气体或超临界流体(常指压力较高时的气体,它具有较大的分子扩散系数和密度,以及较小的粘度)。三个两相共存面相交于SLV线,[kg2] 当[kg2]
当[kg2]
 、
、
 、
、 [kg2]
[kg2] 数值恰好落在此线上时,系统中汽液固三相共存,V、L、S三点分别代表汽相、液相和固相。三个相的温度和压力虽然相等,但它们的摩尔体积各不相同。
数值恰好落在此线上时,系统中汽液固三相共存,V、L、S三点分别代表汽相、液相和固相。三个相的温度和压力虽然相等,但它们的摩尔体积各不相同。在实际应用中,
 -
- -
- 关系常用
关系常用 -
-
 [kg2]
[kg2] 为坐标轴的平面图来表示,这种图称为
为坐标轴的平面图来表示,这种图称为 -
- 图(图2[
图(图2[ -
- 图]
图] -
- 图" class=image>)。图中的虚线是等温线,图上的临界点C,各共存区和各单相区均可与
图" class=image>)。图中的虚线是等温线,图上的临界点C,各共存区和各单相区均可与 -
- -
- 图对照。
图对照。 -
- -
- 关系的数学描述 [kg2]
关系的数学描述 [kg2]
 -
- -
- 关系的基础数据须由实验测得。为了便于应用,常将实验数据关联成某种形式的数学方程,即状态方程。为满足工程计算的需要,还利用对应态原理建立了各种普遍化的
关系的基础数据须由实验测得。为了便于应用,常将实验数据关联成某种形式的数学方程,即状态方程。为满足工程计算的需要,还利用对应态原理建立了各种普遍化的 -
- -
- 关系,如普遍化压缩因子图和普遍化状态方程,它们可近似应用于缺乏实验数据的物质。
关系,如普遍化压缩因子图和普遍化状态方程,它们可近似应用于缺乏实验数据的物质。侯虞钧 谭子明
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条