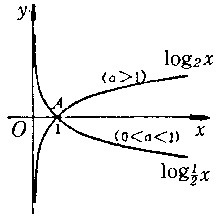1) A(B) type sequence of functions


A(B)型函数序列
2) function spaces of sequentially type


序列型函数空间
1.
The function spaces of sequentially type, which are isometrically isomorphic to some sequence spaces, are described.
描述一类序列型函数空间,它们与某矢量序列空间等距同构,并应用矢量序列空间方法刻划其 Kothe对偶。
3) generating function. graphica sequences


母函数.图型序列
4) function sequence


函数序列
1.
Discussion of linear independence on several complex function sequences


关于几种复杂函数序列的线性无关性的讨论
5) Cantor-like stochastic function sequence


Cantor型随机函数序列
1.
A class of local strong limit theorem for arbitrary Cantor-like stochastic function sequence is investigated.
研究了对任意Cantor型随机函数序列随机和普遍成立的一类局部极限定理。
6) sequence of weight function


权函数序列
补充资料:函数
| 函数 functions 数学中的一种对应关系,是从某集合A到实数集B的对应。简单地说,甲随着乙变,甲就是乙的函数。精确地说,设X是一个不空集合,Y是某个实数集合,f是个规则,若对X中的每个x,按规则f,有Y中的一个y与之对应,就称f是X上的一个函数,记作y=f(x),称X为函数f(x)的定义域,Y为其值域,x叫做自变量,y为因变量。 例1:y=sinx X=[0,2π],Y=[-1,1],它给出了一个函数关系。当然,把Y改为Y1=(a,b),a<b为任意实数,仍然是一个函数关系。 例2:某商场一年12个月毛线的零售量(单位:百千克)变化,见表1。
例3:某河道的一个断面图如图1所示。
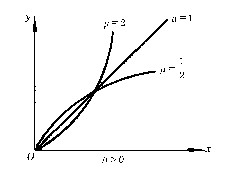
其深度y与一岸边点O到测量点的距离x之间的对应关系呈曲线,这代表一个函数,定义域为[0,b]。以上3例展示了函数的三种表示法:公式法,表格法和图像法。 复合函数 有3个变量,y是u的函数,y=ψ(u),u是x的函数,u=f(x),往往能形成链:y通过中间变量u构成了x的函数: x→u→y,这要看定义域:设ψ的定义域为U。f的值域为U,当U*ÍU时,称f与ψ构成一个复合函数,例如y=lgsinx,x∈(0,π)。此时sinx>0,lgsinx有意义。但如若规定x∈(-π,0),此时sinx<0,lgsinx无意义,就成不了复合函数。 反函数 就关系而言,一般是双向的,函数也如此,设y=f(x)为已知的函数,若对每个y∈Y,有唯一的x∈X,使f(x)=y,这是一个由y找x的过程,即x成了y的函数,记为x=f -1(y)。称f -1为f的反函数。习惯上用x表示自变量,故这个函数仍记为y=f -1(x),例如y=sinx与y=arcsinx互为反函数。在同一坐标系中,y=f(x)与y=f -1(x)的图形关于直线y=x对称。 隐函数 若能由函数方程F(x,y)=0确定y为x的函数y=f(x),即F(x,f(x))≡0,就称y是x的隐函数。 多元函数 设点(x1,x2,…,xn)∈GÍRn,UÍR1,若对每一点(x1,x2,…,xn)∈G,由某规则f有唯一的u∈U与之对应:f:G→U,u=f(x1,x2,…,xn),则称f为一个n元函数,G为定义域,U为值域。 基本初等函数及其图像 幂函数、指数函数、对数函数、三角函数、反三角函数称为基本初等函数。 ①幂函数:y=xμ(μ≠0,μ为任意实数)定义域:μ为正整数时为(-∞,+∞),μ为负整数时是(-∞,0)∪(0,+∞);μ= 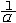 (α为整数),当α是奇数时为(-∞,+∞),当α是偶数时为(0,+∞);μ=p/q,p,q互素,作为 (α为整数),当α是奇数时为(-∞,+∞),当α是偶数时为(0,+∞);μ=p/q,p,q互素,作为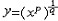 的复合函数进行讨论。略图如图2、图3。 的复合函数进行讨论。略图如图2、图3。
②指数函数:y=ax(a>0,a≠1),定义成为(-∞,+∞),值域为(0,+∞),a>0时是严格单调增加的函数(即当x2>x1时, 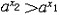 ),0<a<1时是严格单减函数。对任何a,图像均过点(0,1),注意y=ax和y=( ),0<a<1时是严格单减函数。对任何a,图像均过点(0,1),注意y=ax和y=(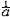 )x的图形关于y轴对称。如图4。 )x的图形关于y轴对称。如图4。
③对数函数:y=logax(a>0),称a为底,定义域为(0,+∞),值域为(-∞,+∞)。a>1时是严格单调增加的,0<a<1时是严格单减的。不论a为何值,对数函数的图形均过点(1,0),对数函数与指数函数互为反函数。如图5。
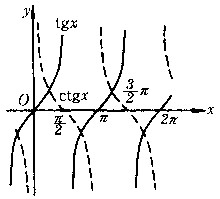
④三角函数:见表2。
正弦函数、余弦函数如图6,图7所示。
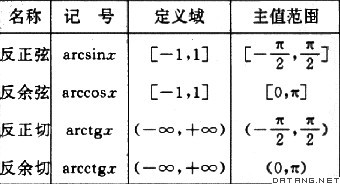
⑤反三角函数:见表3。双曲正、余弦如图8。
⑥双曲函数:双曲正弦 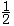 (ex-e-x),双曲余弦(ex+e-x),双曲正切(ex-e-x)/(ex+e-x),双曲余切(ex+e-x)/(ex-e-x)。 (ex-e-x),双曲余弦(ex+e-x),双曲正切(ex-e-x)/(ex+e-x),双曲余切(ex+e-x)/(ex-e-x)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条