1) earth system mechanics
地球系统力学
1.
Preliminary Discussion on Earth System Mechanics (Ⅱ) ——A base of multibody earth system mechanics;
初论地球系统力学(Ⅱ)——多体地球系统力学基础
2.
In this paper, the meaning and content of earth system mechanics are discussed as well as a theory frame is put forward.
地球系统力学是可持续发展战略的科学基础，它跨越一系列自然与社会科学。
2) earth system dynamics
地球系统动力学
3) multibody earth system mechanics
多体地球系统力学
1.
Preliminary Discussion on Earth System Mechanics (Ⅱ) ——A base of multibody earth system mechanics;
初论地球系统力学(Ⅱ)——多体地球系统力学基础
4) earth system dynamic evolution
历史地球系统动力学
5) geodynamic system
地球动力系统
1.
The main features of the geodynamic system have been described.
在分析地球动力系统的主要特征基础上，笔者将地球视为一个自组织临界状态的自然系统，提出一个简单地球热动力系统模型，对地质节律现象进行模拟，并对未来地球动力系统模型要考虑的主要问题进行了简要讨论。
6) earth system science
地球系统科学
1.
Network platform design and development for Earth system science data sharing;
地球系统科学数据共享网络平台的设计和开发
2.
The Earth System Science Partner and Suggestions on China s Development in this Field;
地球系统科学合作伙伴及对我国在该领域发展的建议
补充资料：地球流体力学
| 地球流体力学 geophysical fluiddynamics 研究地球以及其他行星上的自然界流体运动（着重其中大尺度运动）的一般规律学科。是流体力学的一个分支。它是20世纪60年代在流体力学、大气动力学和海洋动力学研究的基础上发展起来的学科。地球流体力学的研究对象具有时间和空间尺度大，星体自旋和引力起重要作用，存在能量输入、交换和耗散过程等特点。地球流体力学目前主要通过建立有关模式来研究大气和海洋的大尺度运动，并研究支配这些运动的基本方程、基本运动形态和基本动力学过程。 基本方程 一般的流体力学基本方程组（流体运动所遵循的物理规律的数学表达式）也适用于地球流体力学，但须考虑具体条件进行适当的修改。 ①拉普拉斯潮汐方程组。P.-S.拉普拉斯最早以流体动力学观点研究海洋潮汐，他所使用的偏微分方程组也是地球流体力学的基本方程组。它们由正压原始方程组略去非线性项得出，说明潮汐的本质是由引潮力引起的波动。它们是描写流体在重力和科里奥利力作用下运动状况的基本方程组 ，推广用于三维问题时，还可解释大气中（尤其是平流层以上高空）的大气潮汐现象（由月球引力和太阳的引力及辐射所引发的大气日变化）。 ②斜压原始方程组。描述大气和海洋三维大尺度运动的基本方程组。通过它可以研究外界能流对自然界流体运动的影响。此方程组是基本的，但很复杂，有待进一步简化。 ③位涡量守恒方程。由正压原始方程组导出的一个方程，说明在理想流体中每个质点的位涡量守恒。该方程比原始方程更便于作理论研究。 基本相似准数 最重要的有罗斯比数和埃克曼数。 ①罗斯比数R0。表征惯性力与科里奥利力之比的流体力学相似准数，由芝加哥气象学派为纪念其创立者C.-G.A.罗斯比而取名，但此数实由前苏联气象学家H.A.基别尔最先引入，故又常称罗斯比-基别尔数。其定义为R0＝U／fL，其中U、L为流体水平运动的特征速度和特征长度；f＝2Ωsinj为科里奥利参数，Ω为行星自旋角速度，j为纬度。在地面上R0 ＜＜ 1时，科里奥利力起主导作用，流动呈准地转特征；R0≈1时，惯性力不可忽略，流动呈非地转特征。 ②埃克曼数Ek。表征耗散力（粘性力）与科里奥利力之比的流体力学相似准数，为纪念海洋学家V.W.埃克曼而命名。其定义为Ek＝k／fD2，其中k 为耗散系数；f为科里奥利参数；D 为运动在铅直方向的特征长度 。在靠近地球表面或其他行星固体表面厚度为 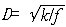 的流体层内有Ek≈ 1，耗散力和科里奥利力同等重要，形成行星边界层。埃克曼数主要用于研究耗散力和科里奥利力都起作用的旋转流场中的边界层流动，如受地球自转影响的大气边界层或其他行星边界层流动，流体机械中旋转叶片的边界层流动等。运动的分类 地球流体运动包括重力-惯性波、行星波、埃克曼流、大气和大洋环流、涡旋、重力波和对流等。后三者为一般流体力学所共有，这里不单独解释。 ① 重力-惯性波。地球流体的一种基本运动形式，由重力和科里奥利力共同作用所形成。相速（见波）远大于流速。若波长较短，则科里奥利力影响极小，与通常分层流动中的重力波无异。若波长较长，特别是和地球（或别的行星）同量级时，科里奥利力影响明显，则波的相速和结构都与重力波明显不同。 ②行星波。地球的大气运动、海洋运动和其他行星大气大尺度运动的最明显和最重要的形式，流场弯曲如波状，波长大都与行星半径同量级（在洋流中波长较短），因而得名。又称罗斯比 - 阿尔文波或罗斯比波。行星波与大型天气系统密切相关，又是大气环流或大洋环流的主要组成部分，故为大气动力学 、海洋动力学和地球流体力学的主要研究对象。行星波的相速和流速同量级，涡量远大于散度，故又称涡旋波。其产生机制是行星表面各处的科里奥利参数不均匀，即行星大气涡量的地面法向分量存在梯度，从而使流体微团在运动过程中改变其相对涡量，形成波动。 ③埃克曼流。行星边界层内的流动。其主要特征是流体速度水平分量沿高度呈螺线变化，称埃克曼螺线。这是由于层内流体速度因粘性力作用而减小，使科里奥利力与压强梯度 、重力之间失去平衡的结果 。埃克曼流常伴有铅直速度，称埃克曼抽吸，影响行星边界层外的大尺度运动。 ④大气环流。大气中各种大尺度运动的全体组成的具有最大空间尺度的运动 。 已发现两种非常不同的大气环流型：罗斯比环流型，由明显的行星波组成的非轴对称的大气环流型，为纪念阐明行星波的罗斯比而命名。地球大气环流即属此型；哈得莱环流型，对星体自旋轴对称和准对称的大气环流型。由G.哈得莱首先阐明而得名。木星大气环流即属此型。大气环流型主要取决于行星自转角速度Ω以及行星大气受太阳辐射而造成极地和赤道之间的温差｜ΔΤ｜。 ⑤大洋环流。地球上海洋中各种大尺度运动的全体组成的最大空间尺度的运动 。大洋环流和大气环流有许多共性，但海岸的几何约束对洋流有明显影响，使其具有特点。最简单的一种大洋环流模式是惯性洋流。在这种模式中，风应力、科里奥利力和惯性力三者互相平衡。在开阔洋面上，洋流为风应力所驱动，然后受惯性力作用流向海岸地带，科里奥利力随纬度的变化使向西流动的 洋流加速 ，称西向强化现象；子午线走向的海岸的几何约束，使洋流转而流向高纬地区并强化（北向强化现象）。这是大西洋湾流和太平洋暖流（即黑潮）的显著特点。 地球流体运动也常按科里奥利力影响的程度分为准地转运动和非地转运动两大类： ①准地转运动。满足Ro＜＜1和Ek＜＜1的运动。在这类运动中，重力、压强梯度力和科里奥利力三者几乎平衡，且运动为准水平的，沿重力方向的速度分量很小。大气和海洋环流、行星波以及大尺度涡旋属于准地转运动，是地球流体大尺度运动的主要类型。 ②非地转运动。除准地转运动外的地球流体运动。在这类运动中，重力、压强梯度力和科里奥利力三者不处于几乎平衡状态 。在自由流体中 ，Ro ＜＜1不成立。重力-惯性波、重力波、对流、尺度较小的强涡旋和埃克曼流属于非地转运动。 基本动力过程 支配地球流体大尺度运动的动力过程有地转适应过程和准地转演变过程等。 ①地转适应过程。使地球流体非地转运动很快地调整为准地转运动的动力过程。若局部地区有非地转运动，则重力波和重力-惯性波的能量很快地沿水平和垂直方向弥散 ，而科里奥利力作用则使运动较快地变为准地转运动。这就是地转适应过程的实质，也是使地球流体大尺度运动经常保持为准地转运动的重要机理。 ②准地转演变过程。准地转运动随时间变化的动力过程。控制此过程的因子是涡量或位涡量沿空间分布的不均匀、能源）和耗散力。大气动力学、海洋动力学和地球流体力学着重研究准地转演变过程。天气形势预报就是根据对天气系统（大尺度大气流场）的准地转演变过程的研究结果作出的。 准地转模式 描写准地转运动的动力学的理论模式。在数学上它用一个只含流函数的偏微分方程描写，这个方程也常被称为准地转模式。引入流函数并将速度场、温度场和压强场等按罗斯比数展开，代入位涡量守恒方程，只取零级近似，即得准地转模式。在地球流体力学中，对准地转模式研究得最多，应用也最广。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条