1) binary-flow network


双流网络
2) Double-flow Increment Network


双流增量网络
3) double-loop network


双环网络
1.
Equivalent span-tree of double-loop network G(N;1,s);


双环网络G(N;1,s)等价生成树
2.
This paper analyzes a kind of double-loop networks DL(N, h), where the greatest common divisor is equal to h.
对双环网络DL(N,h)(满足最大公因数 g( N,h)=h)进行了分析,证明了这类双环网络中最短路径形式唯一且可用简单的数学表达式来描述,给出了最短路径的公式。
3.
The shortest [+h]-link prior path and the bamboo raft(a new kind of L-shaped Tile)for a double-loop network are obtained.
提出一种先走[+h]边、当走[+h]边不利时才走[+1]边的[+h]边优先寻径策略;得出[+h]边优先最短路径和双环网络的"竹筏"(一种新L形瓦)型空间解;"竹筏"中节点之间的[+h]边优先最短路径存在递推关系;由节点的[+h]边优先最短路径推出双环网络的直径公式;利用VB6。
4) two-port network


双口网络
1.
The types of interconnection of two-port networks are: series,parallel,series-parallel,parallel-series and cascade connection.
一些功能不同的双口网络适当地连接在一起会实现某种特定的功能。
2.
Considering the changes of a power system in topology and on the basis of the two-port network theory, a fast method to calculate the open-port voltage of positive sequence network during a large-scale power system oscillation, which is caused by asymmetrical open-conductor faults, is presented.
基于双口网络理论 ,对继电保护整定计算过程中大型电力系统非全相振荡时任意时刻正序网断相口开路电压的计算方法进行了深入研究 ,提出了一种能自动适应电力系统网络操作 ,可快速计算大型电力系统非全相振荡时任意时刻正序网断相口开路电压的新方法 ,并应用这一方法解决了继电保护整定计算中快速计算大型电力系统非全相振荡时任意时刻电气量的问题。
3.
tuner or the televisor in VHF band by the theory of Two-port network and filter.


本文应用双口网络及滤波器理论系统地讨论了电视机VHF频段高频调谐器中输入带通滤波器的原理及设计。
5) double-loop networks


双环网络
1.
On tight optimal double-loop networks G(N;r,s) with non-unit step;


关于非单位步长的紧优双环网络G(N;r,s)
2.
Bintree-based shortest path algorithm of directed double-loop networks


基于二叉树的有向双环网络的最短路径算法
3.
Research on double-loop networks G(N;r,s) of span-tree


等价树的双环网络G(N;r,s)的研究
6) double layer network


双层网络
1.
Discussed the concept of GSM-R double layer network,analyzed and compared different designs of GSM-R double layer network,proposed network design suggestions according to different line,and analyzed active-standby and load sharing in GSM-R network.
阐述了GSM-R双层网络的概念,分析比较了GSM-R双层网络的各种设计方案,针对不同铁路线路提出了设计建议,并对双层网络中主备用和负荷分担2种工作方式进行了研究。
补充资料:网络流
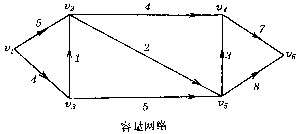
| 网络流 network flows 图论中的一种理论与方法,研究网络上的一类最优化问题。1955年,T.E.哈里斯在研究铁路最大通量时首先提出在一个给定的网络上寻求两点间最大运输量的问题。1956年,L.R.福特和D.R.富尔克森等人给出了解决这类问题的算法,从而建立了网络流理论。所谓网络或容量网络指的是一个连通的赋权有向图D=(V、E、C),其中V是该图的顶点集,E是有向边(即弧)集,C是弧上的容量。此外顶点集中包括一个起点和一个终点。网络上的流就是由起点流向终点的可行流,这是定义在网络上的非负函数,它一方面受到容量的限制,另一方面除去起点和终点以外,在所有中途点要求保持流入量和流出量是平衡的。如果把下图看作一个公路网,顶点v1…v6表示6座城镇,每条边上的权数表示两城镇间的公路长度。现在要问:若从起点v1将物资运送到终点v6去,应选择那条路线才能使总运输距离最短这样一类问题称为最短路问题。如果把上图看作一个输油管道网,v1表示发送点,v6表示接收点,其他点表示中转站,各边的权数表示该段管道的最大输送量。现在要问怎样安排输油线路才能使从v1到v6的总运输量为最大这样的问题称为最大流问题。
最大流理论是由福特和富尔克森于1956年创立的,他们指出最大流的流值等于最小割(截集)的容量这个重要的事实,并根据这一原理设计了用标号法求最大流的方法,后来又有人加以改进,使得求解最大流的方法更加丰富和完善。最大流问题的研究密切了图论和运筹学,特别是与线性规划的联系,开辟了图论应用的新途径。 最大流问题仅注意网络流的流通能力,没有考虑流通的费用。实际上费用因素是很重要的。例如在交通运输问题中,往往要求在完成运输任务的前提下,寻求一个使总运输费用最省的运输方案,这就是最小费用流问题。如果只考虑单位货物的运输费用,那么这个问题就变成最短路问题。由此可见,最短路问题是最小费用流问题的基础。现已有一系列求最短路的成功方法。最小费用流(或最小费用最大流)问题,可以交替使用求解最大流和最短路两种方法,通过迭代得到解决。 目前网络流的理论和应用在不断发展,出现了具有增益的流、多终端流、多商品流以及网络流的分解与合成等新课题。网络流的应用已遍及通讯、运输、电力、工程规划、任务分派、设备更新以及计算机辅助设计等众多领域。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条