1) typical resolving

典型分解
1.
The typical resolving theorem of finite dimensional time\|invariant linear system is one of the important results of control theory [1] and one of the important bases of computer control theory as well.
有限维线性定常系统的典型分解定理是控制理论的重要成果之一 [1] ,也是计算机控制的重要理论基础之一 ,本文将这一结果推广到 Hilbert空间上的无限维线性定常系统 。
2) canonical flabby resolution

典型松弛分解
3) Fading of vogue of typical role

消解典型
4) typolysis

典型溶解
5) non-classical modal superposition

非经典振型分解法
6) typical stands

典型林分
1.
Runoff generation characteristics on three time scales for typical stands in Jinyun Mountain,Chongqing City;
重庆缙云山典型林分3种时间尺度下产流特征研究
补充资料:AutoCAD典型应用技巧五则
AutoCAD在中国的应用已经有很多年了,这里再次谈到它的应用技巧似乎有些老生常谈。但编辑还是想把这篇文章介绍给广大读者朋友们,因为掌握好软件的应用技巧,不但能够提高自身的设计水平,还可以大大地提高设计效率的,是有百益而无一害的。
在计算机辅助设计软件中,AutoCAD无疑是应用最普遍的,每个工程技术人员都有一些自己的使用经验。其中有些经验不易直接从书籍获取,也难靠自己摸索得来。下面介绍笔者多年来积累的一些教学经验技巧,在实际应用中合理地使用这些技巧能大大提高绘图的效率和质量。
一、妙用夹点编辑命令
在使用夹点编辑命令时,很多人把该命令仅仅当成STRETCH(拉伸)、MOVE(移动)、ROTATE(旋转)、SCALE(缩放)和MIRROR(镜像)等单个命令的简单重复。实际上,如果灵活运用该命令中丰富的编辑方式并巧妙组合,能大大提高绘图效率。基于AutoCAD较强的实践性,现以图1为例,说明夹点编辑命令的巧妙运用。步骤如下:
1.作直径为1的半圆;
2.在Command状态下,拾取半圆,激活左或右端点为关键点,待命令行出现拉伸提示时,按三次回车键至比例缩放,选择复制选项并依次输入比例缩放因子1/6、2/6、3/6、4/6、5/6;
3.再次运用夹点编辑命令中的旋转结合复制将前两步绘制出的图形旋转180°即可。(注意:此时关键点选择为直径为1的半圆的圆心)
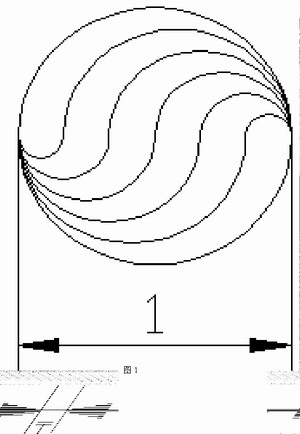
图1 用夹点编辑命令绘制圆形
二、矩形倒圆(直)角命令的应用
AutoCAD创建矩形,一般采用直接输入长宽的数值或选择端点的方式来完成。实际上,还可以利用矩形命令里倒直角或圆角的方式高效快速地绘制带有直角或圆角的图形。点击“矩形”按钮或输入“rec”命令后,首先根据提示选择“f”或“c”参数,确定圆角半径或直角距离,再输入矩形的长和宽即可。现以图2为例,说明矩形倒圆(直)角命令的巧妙运用。
1.点击“矩形”按钮或输入“rec”;
2.根据提示选择“f”参数,输入半径为10;
3.指定第一个角点后,输入矩形长宽的相对坐标即“@40,20”。
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条





