1) plane-movement energy of particles


质心平动动能
2) barycentric energy of motion


质心动能
1.
This paper discusses that the barycentric energy of motion can be changed by the work of endogenous force in mass points group and also presents the condition for that.
讨论了质点组内力的功是可以改变质心动能的 ,以及所满足的条
3) translational kinetic energy


平动动能
1.
It is pointed out that translational kinetic energy and rotational kinetic energy mutually transferred by sliding friction force, but it only has positive acting.
讨论滑动摩擦力作功,说明了滑动摩擦力可以使刚体的平动动能和转动动能之间相互转换,但总是作负功。
2.
The variation curves of rotational kinetic energy and translational kinetic energy changing with angle coordinate are drawn using MATLAB.
建立了摆的动力学方程,导出了动能定理的微分表达式和积分表达式,用MATLAB软件编程画出了转动动能、平动动能与角坐标间的关系曲线,分析了平动动能对振动周期的影响。
4) barycentric momentum


质心动量
5) Moving mass vehicle


移动质心
6) barycentric oscillation


质心摆动
补充资料:质心
| 质心 mass,centre of 质点系质量分布的平均位置。质量中心的简称。它同作用于质点系上的力系无关。设n个质点组成的质点系,其各质点的质量分别为m1,m2,…,mn。若用r1,r2,…,rn分别表示质点系中各质点相对某固定点的矢径,rc表示质心的矢径,则有rc=  miri/ miri/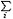 mi。当物体具有连续分布的质量时,质心C的矢径rc= mi。当物体具有连续分布的质量时,质心C的矢径rc= ρrdτ/ ρrdτ/ ρdτ,式中ρ为体(或面、线)密度;dτ为相当于ρ的体(或面、线)元;积分在具有分布密度ρ的整个物质体(或面、线)上进行。由牛顿运动定律或质点系的动量定理,可推导出质心运动定理:质心的运动和一个位于质心的质点的运动相同,该质点的质量等于质点系的总质量,而该质点上的作用力则等于作用于质点系上的所有外力平移到这一点后的矢量和。由这个定理可推知:①质点系的内力不能影响质心的运动。②若质点系所受外力的主矢始终为零, 则其质心作匀速直线运动或保持 静止状态。③若作用于质点系上外力的主矢在某一轴上的投影始终为零,则质心在该轴上的坐标匀速变化或保持不变。质点系的任何运动一般都可分解为质心的平动和相对于质心的运动。质点系相对某一静止坐标系的动能等于质心的动能和质点系相对随质心作平动的参考系运动的动能之和。质心位置在工程上有重要意义,例如要使起重机保持稳定,其质心位置应满足一定条件;飞机、轮船、车辆等的运动稳定性也与质心位置密切相关;此外,若高速转动飞轮的质心不在转动轴线上,则会引起剧烈振动而影响机器正常工作和寿命。 ρdτ,式中ρ为体(或面、线)密度;dτ为相当于ρ的体(或面、线)元;积分在具有分布密度ρ的整个物质体(或面、线)上进行。由牛顿运动定律或质点系的动量定理,可推导出质心运动定理:质心的运动和一个位于质心的质点的运动相同,该质点的质量等于质点系的总质量,而该质点上的作用力则等于作用于质点系上的所有外力平移到这一点后的矢量和。由这个定理可推知:①质点系的内力不能影响质心的运动。②若质点系所受外力的主矢始终为零, 则其质心作匀速直线运动或保持 静止状态。③若作用于质点系上外力的主矢在某一轴上的投影始终为零,则质心在该轴上的坐标匀速变化或保持不变。质点系的任何运动一般都可分解为质心的平动和相对于质心的运动。质点系相对某一静止坐标系的动能等于质心的动能和质点系相对随质心作平动的参考系运动的动能之和。质心位置在工程上有重要意义,例如要使起重机保持稳定,其质心位置应满足一定条件;飞机、轮船、车辆等的运动稳定性也与质心位置密切相关;此外,若高速转动飞轮的质心不在转动轴线上,则会引起剧烈振动而影响机器正常工作和寿命。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条