1) Interpolating(Strictly Interpolating)Subspace


插值(严格插值)子空间
2) spatial interpolation


空间插值
1.
Buildup and application of multi-factor spatial interpolation model in the monitoring and warning system for crop diseases and insect pests;
多因子空间插值模型在农作物病虫害监测预警系统中的构建及应用
2.
Potential land productivity calculation in foothill and mountain area based on GIS and spatial interpolation technology;
基于GIS和空间插值技术的南方丘陵山区土地生产潜力估算
3.
Optimization of the spatial interpolation for marine phytoplankton abundance;


海洋浮游植物丰度的空间插值优化
3) space interpolation


空间插值
1.
From this point of view,RBF neural network to space interpolation is introduced.


根据RBF网络能以任意精度逼近任意函数这一特性,将RBF网络应用于空间插值,认定地表空间坐标的空间分布可以用一复杂的非线性函数模拟。
2.
With the analyses of the space interpolation algorithms,the contour generation algorithm based on mobile camber fitting was discussed.
对现有空间插值算法进行了分析,探讨了基于移动曲面拟合等高线生成算法,优化了等高线线性内插和平滑输出的算法,编写了基于VC++的拟合等高线程序,通过模拟数据生成等高线实验,分析了算法的优缺点,探讨了生成等高线的精度。
3.
Furthermore, the vohume of hemorrhage parts is computed with the space interpolation method.
通过对颅内组织及出血部位CT值特性的正确分析 ,在对原始CT图像进行一系列的处理 :滤波、增强、二值化的基础上 ,用模式识别中最优阀值的方法 ,实现了对出血部位的正确分割 ,并通过空间插值的方法 ,较精确地计算出血部位的体积 。
4) interpolation
[英][in,tə:pəu'leiʃən] [美][ɪn,tɚpə'leʃən]


空间插值
1.
Soil potassium spatial variability and comparison of several interpolation methods;


土壤钾素空间变异性和空间插值方法的比较研究
2.
Application of the spatial interpolation of rainfall——A case study of the headstream region of the Yellow River;
降水空间插值方法应用研究——以黄河源区为例
6) interpolation
[英][in,tə:pəu'leiʃən] [美][ɪn,tɚpə'leʃən]


网格插值
1.
The paper introduces the calculation method of surface rainfall amoun t with grid interpolation method, compares and analyses isoline chart firmed by grid points and observed rainfall isoline chart, so rainfall amount value after interpolation is trustworthy.
本文介绍了利用网格插值计算流域面雨量的方法,并对由网格点生成的雨量等值线图和实测雨量生成的雨量等值线图进行分析比较,验证了插值后雨量值的可信性。
补充资料:插值
| 插值 interpolation 在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点。插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值状况,估算出函数在其他点处的近似值。 早在6世纪,中国的刘焯已将等距二次插值用于天文计算。17世纪之后,I.牛顿,J.-L.拉格朗日分别讨论了等距和非等距的一般插值公式。在近代,插值法仍然是数据处理和编制函数表的常用工具,又是数值积分、数值微分、非线性方程求根和微分方程数值解法的重要基础,许多求解计算公式都是以插值为基础导出的。 插值问题的提法是:假定区间[a,b]上的实值函数f(x)在该区间上 n+1个互不相同点x0,x1……xn 处的值是f [x0],……f(xn),要求估算f(x)在[a,b]中某点 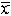 的值。其做法是:在事先选定的一个由简单函数构成的有n+1个参数C0,C1,……Cn的函数类Φ(C0,C1,……Cn)中求出满足条件P(xi)=f(xi)(i=0,1,…… n)的函数P(x),并以P( 的值。其做法是:在事先选定的一个由简单函数构成的有n+1个参数C0,C1,……Cn的函数类Φ(C0,C1,……Cn)中求出满足条件P(xi)=f(xi)(i=0,1,…… n)的函数P(x),并以P(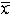 )作为f( )作为f(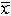 )的估值。此处f(x)称为被插值函数,c0,x1,……xn称为插值结(节)点,Φ(C0,C1,……Cn)称为插值函数类,上面等式称为插值条件,Φ(C0,……Cn)中满足上式的函数称为插值函数,R(x)= f(x)-P(x)称为插值余项。当估算点 )的估值。此处f(x)称为被插值函数,c0,x1,……xn称为插值结(节)点,Φ(C0,C1,……Cn)称为插值函数类,上面等式称为插值条件,Φ(C0,……Cn)中满足上式的函数称为插值函数,R(x)= f(x)-P(x)称为插值余项。当估算点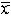 属于包含x0,x1……xn的最小闭区间时,相应的插值称为内插,否则称为外插。 属于包含x0,x1……xn的最小闭区间时,相应的插值称为内插,否则称为外插。多项式插值 这是最常见的一种函数插值。在一般插值问题中,若选取Φ为n次多项式类,由插值条件可以唯一确定一个n次插值多项式满足上述条件。从几何上看可以理解为:已知平面上n+1个不同点,要寻找一条n次多项式曲线通过这些点。插值多项式一般有两种常见的表达形式,一个是拉格朗日插值多项式,另一个是牛顿插值多项式。 埃尔米特插值 对于函数f(x),常常不仅知道它在一些点的函数值,而且还知道它在这些点的导数值。这时的插值函数P(x),自然不仅要求在这些点等于f(x)的函数值,而且要求P(x)的导数在这些点也等于f(x)的导数值。这就是埃尔米特插值问题,也称带导数的插值问题。从几何上看,这种插值要寻求的多项式曲线不仅要通过平面上的已知点组,而且在这些点(或者其中一部分)与原曲线“密切”,即它们有相同的斜率。可见埃尔米特插值多项式比起一般多项式插值有较高的光滑逼近要求。 分段插值与样条插值 为了避免高次插值可能出现的大幅度波动现象,在实际应用中通常采用分段低次插值来提高近似程度,比如可用分段线性插值或分段三次埃尔米特插值来逼近已知函数,但它们的总体光滑性较差。为了克服这一缺点,一种全局化的分段插值方法——三次样条插值成为比较理想的工具。见样条函数。 三角函数插值 当被插函数是以2π为周期的函数时,通常用n阶三角多项式作为插值函数,并通过高斯三角插值表出。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条