1) Triangle and triangle intersection test


三角形和三角形相交测试
2) triangle-triangle intersection test


三角形对相交测试
1.
To improve the response speed of collision detection, it is necessary to reduce the steps and complexity of triangle-triangle intersection test.
而基本几何元素大多是三角形或四面体,因此高效的三角形对相交测试对提高碰撞检测算法效率,增强动画场景中的真实感起着至关重要的作用。
3) intersecting triangles


相交三角形
1.
Total coloring of plane graphs with maximum degree six and without intersecting triangles and 4-cycles
最大度为6不含相交三角形和4-圈的平面图的全染色
2.
It was proved that a plane graph with maximum degree Δ=6 and without intersecting triangles were 8 totally colorable by discharging.
用Discharging方法证明了最大度Δ=6且不含相交三角形的平面图是8全可染的。
4) triangle intersection


三角形求交
5) similar triangle


相似三角形
1.
Dissections of regular polygons into similar triangles;


正多边形的相似三角形划分
2.
In order to overcome the common problem in fingerprint recognition,a fingerprint minutia matching algorithm based on improved similar triangle is proposed.
为了克服指纹识别中的常见问题,提出了一种基于改进的相似三角形的指纹细节点匹配算法。
6) homothetic triangle


相似三角形
1.
Based on homothetic triangle theory,a new height computation method of pile type brige pier and ribbed plate type abutment post is introduced.
文章以一种新的思维方式-相似三角形原理计算桩柱式桥墩、肋板式桥台柱(肋板)顶高程。
补充资料:三角学
| 三角学 trigonometry 研究平面三角形和球面三角形边角关系的数学学科。三角学起源于古希腊。为了预报天体运行路线、计算日历、航海等需要,古希腊人已研究球面三角形的边角关系,掌握了球面三角形两边之和大于第三边,球面三角形内角之和大于两个直角,等边对等角等定理。印度人和阿拉伯人对三角学也有研究和推进,但主要是应用在天文学方面。15、16世纪三角学的研究转入平面三角,以达到测量上应用的目的。16世纪法国数学家F.韦达系统地研究了平面三角。他出版了应用于三角形的数学定律的书。此后,平面三角从天文学中分离出来,成了一个独立的分支。平面三角学的内容主要有三角函数、解三角形和三角方程。
三角学中的三角函数有6个,是用几何方法定义的。在直角坐标系中,设以射线Ox为始边,OP为终边的角为θ,P点的坐标为(x,y),|OP|=r,这时6个比 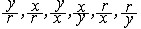 由θ的大小确定,都是θ的函数,称它们为角θ的三角函数,分别记作 由θ的大小确定,都是θ的函数,称它们为角θ的三角函数,分别记作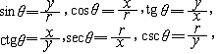
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
||
| ©2011 dictall.com | ||
