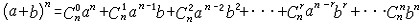1) matrix binomial function


矩阵二项式定理
2) binomial theorem


二项式定理
1.
Deduction of pythagorean triple group formula and double angle formula by using binomial theorem;
利用二项式定理推导勾股数组公式和倍角公式
2.
It is known that binomial theorem provides the expansion type of the nth power of the wum of two numbers.
二项式定理给出了两数之和的n次幂的展开式(n为正整数),文中研究了当n趋于无穷时展开式系数的分布趋势,并给出了一个应用实例。
3.
This paper provides a method that binomial theorem applied in the algebra changes the question of state feedback抯 pole configuration on second-order system of higher-order into algebra computation.
该文提供一种方法,当被控对象为高阶二次环节时,可运用代数学中普遍应用的二项式定理,将高阶二次环节的状态反馈极点配置问题的矩阵运算转换成代数运算,从而简化状态反馈极点配置问题的求解过程。
3) uncertain polynomial matrices


不确定多项式矩阵
4) polynomial matrix


多项式矩阵
1.
In this paper, the concepts of the least common multiple of polynomial matrices and the prime polynomial matrix are introduced, and some algebraic properties of the greatest common divisor and of the least common multiple of polynomial matrices are given.
讨论了多项式矩阵最大公因子与最小公倍的有关性质,同时给出了多项式矩阵的分解定理。
2.
Based on the theory of polynomial matrix,it is implied that the right coprime of polynomialmatrices of the autoregressive part and moving-average part is only the necessary condition,not the suf-ficient condition to ensure that the model is the normalized form.
本文从多项式矩阵理论入手,指出多维时序模型的自回归部分多项式矩阵与滑动平均部分的多项式矩阵右互质,只是保证模型为典则型的必要条件,而不是充分条件,因此,为了获得多变量时序模型的典则型,必须限制模型的部分参数表达形式,因此提出了一种形式简单的多变量时序模型的典则型,并给出了实现的具体算法,还证明了该典则型自回归与滑动平均部分的多项式矩阵是右互质的。
5) matrix polynomial


矩阵多项式
1.
On square-rooting matrices of a kind of matrix polynomial


一类矩阵多项式的平方根矩阵问题
2.
The frequency criteria for Schur stability of matrix polynomials without expanding the determinants of the matrix polynomials has been proposed.
提出矩阵多项式Schur稳定的频域判据 ,可避免矩阵多项式的行列式展开 ,使多输入多输出离散时滞系统稳定性检验得以简
3.
Based on this,some identities of the rank of a class of matrix polynomials were obtained.


给出了矩阵秩的Frobenius不等式取等号的一个充分条件,在此基础上获得了一类矩阵多项式秩的恒等式。
6) matrix theorem


矩阵定理