1) generalized energy-momentum tensor


广义能量动量张量
2) generalized energy-moment of momentum tensor


广义能量动量矩张量
4) generalized momentum


广义动量
1.
The equation of motion for a particle is derived from the Hamilton s principle in a covariant vector form and the generalized momentum for a relativistic particle is given.
从协变形式的Hamilton原理得到粒子的运动方程 ,给出相对论性粒子广义动量用协变矢量表示的正确形式 ,并讨论了电磁场中带电粒子系统的哈密顿函数 ,指出一些文献中不当之处。
2.
A conservation law of generalized momentum is derived by solving the semi analytical governing equation of elasticity in the Hamilton system,and the conservation of generalized momentum in various cases is discussed in detail.
通过对Hamilton体系下弹性力学半解析法控制方程的求解 ,得到了一个广义动量守恒定律 ,并较为详细地讨论了单元不等长、一边有面力或有位移边界、有体力等情况的广义动量守恒性 。
3.
Calculations show that relation is determined by the dimensions of space and powers of generalized momentum for particle energy spectrum.
研究理想气体内能和态式的一种关系 ,计算表明二者之间的关系由空间维数和粒子能量中广义动量的幂数决
5) energy-momentum tensor


能动张量
1.
The renormalized energy-momentum tensor and Casimir effect of Dirac field in two-dimensional static spacetime;
二维静态时空中Dirac场的重正化能动张量和Casimir效应
6) energy-momentum tensor


能量动量张量
1.
Two potential dual theory of EM field energy-momentum tensor;


电磁场能量动量张量的双矢势对偶理论
补充资料:广义动量
| 广义动量 generalized momentum 用广义速度表示的完整系统(见约束)的动能T对广义速度的偏导数。它可表达为 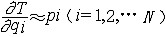 ,即对应于N个广义坐标 qi(i= 1,2…,N )有N个广义动量pi(i=1,2,…,N)。当qi为线量时,pi就是(线)动量;当q为角量时,p就是角动量。若系统是保守系统且系统的拉格朗日函数 L不显含时间t,则L=T-V,H=T+V,其中V为势函数 ;H为哈密顿函数 。因 V 只是广义坐标的函数,所以 ,即对应于N个广义坐标 qi(i= 1,2…,N )有N个广义动量pi(i=1,2,…,N)。当qi为线量时,pi就是(线)动量;当q为角量时,p就是角动量。若系统是保守系统且系统的拉格朗日函数 L不显含时间t,则L=T-V,H=T+V,其中V为势函数 ;H为哈密顿函数 。因 V 只是广义坐标的函数,所以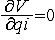 ,于是广义动量又常可写为 ,于是广义动量又常可写为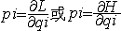 。 。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条