1) wide Gougu equation


广勾股方程
2) Pythagorean equation


勾股方程
1.
This article gives out a method which used basic solutions of Pythagorean equation to solve this question completely.
本文利用勾股方程的基本解 ,完全解决了这一问
3) right triangular diophantine equation


勾股丢番图方程
1.
In this paper, the integer solutions and rational solutions of the right triangular diophantine equation aregiven and generalized to the solutions of diophantine equation x_1~2+x_2~2+…x_n~2=y~2.
给出了勾股丢番图方程的整数解和有理数解,并推广至二次齐次丢番图方程的求解。
5) Pythagorean inverse theorem in wider sense


广义勾股逆定理
6) pythagorean orthogonality


勾股正交
1.
In this paper we carefully investigated some relationships between Birkhoff orthogonality duality map, and isosceles orthogonality, pythagorean orthogonality, and Roberts orthogonality, some characteristics of inner product spaces are also given.
讨论了Birkhoff正交性与对偶映射、等腰正交性、勾股正交性和Roberts正交性之间联 系,给出了内积空间的特征性质。
补充资料:勾股定理
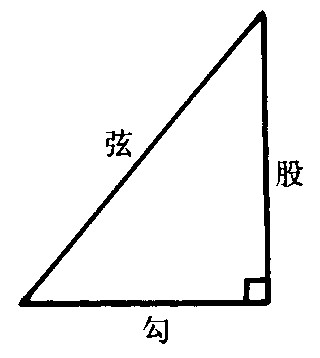
| 勾股定理 中国古代算理之一。文字记载见于成书于公元前1世纪的古文献《周髀算经》中。中国古代称直角三角形为勾股形,两条直角边称为勾、股,斜边称为弦(见图),且勾2+股2=弦2,满足这个条件的正整数组叫勾股数组,《周髀算经》中给出一组勾股数组,即勾三股四弦五。此后的《九章算术》中,又给出另外4组勾股数组,即5,12,13;7,24,25;8,15,17;20,21,29。古希腊的毕达哥拉斯学派对勾股数也有研究,其成果载于欧几里得的《几何原本》。所以,西方数学文献中称勾股数为毕达哥拉斯数。
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条