2) spatial cohesion
空间离散度
1.
Secondly,to provide geometric invariant image matching,annular color histogram and spatial cohesion based on interest points are presented to describe image features.
该方法把图像内容看作为由若干兴趣点组成的集合,首先利用小波系数的空间方向树特性来检测兴趣点,然后利用基于兴趣点的环形颜色直方图和空间离散度来描述图像的特征,最后用加权特征距离来估计图像内容的相似度。
3) accuracy of spatial discretizations
空间离散精度
1.
On the base of scalar USLIP scheme,the paper analyses the relations between flux limiters and accuracy of spatial discretizations.
本文从标量形式的ＵＳＬＩＰ格式出发，从理论上分析了通量限制器与ＬＥＤ（Ｌｏ－ｃａｌＥｘｔｒｅｍ ｕｍ Ｄｉｍ ｉｎｉｓｈｉｎｇ）性质和空间离散精度的关系。
4) spatial distribution dispersion
空间分布离散度
5) discrete space
离散空间
1.
It′s topological properties are studied,three equivalent conditions of which topological space(E,T) is discrete space and one equivalent condition of which topological space(E,T) is mediocre space are abtained.
以离散参数马尔可夫链状态空间E为集合定义该集合上的一个拓扑T,研究它的拓扑性质,得到拓扑空间(E,T)是离散空间的三个等价刻画以及(E,T)是平庸空间的一个等价刻画。
2.
A hierarchical MAS (multi-agent system) based on a multi-level discrete space and mesoscopic agent model for signal transduction network modeling and simulation was proposed.
提出一种基于多层次离散空间和介观水平Agent的层次式多Agent系统仿真细胞信号转导网络。
补充资料：度量空间
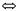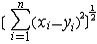| 度量空间 metric space 具有度量的抽象空间，设X是一个集合，若有定义在X×X上的非负实值函数d，满足①d（x，y）≥0，d（x，y）＝0  x＝y； ②d（x，y）＝d（y，x）；③d（x，z）≤d（x，y）＋d（y，z），则称（X，d）是度量空间，d称为距离或度量。这是最接近于欧几里得空间的抽象空间。利用度量可很自然地将欧几里得空间上点的邻域、开集、闭集，收敛序列以及连续映射等概念推广到一般度量空间，也能将一致连续的概念推广到度量空间。由于19世纪末集合论产生后，实变函数及泛函分析的发展，需要规定函数间的距离，因而抽象出度量、度量空间的概念，其创始人是M.R.弗雷歇。常见的度量空间有：n维欧几里得空间（Rn,d）：Rn＝｛（x1，…，xn）｜xi∈R，i＝1，2，…，n ｝，d（x，y）＝  ，其中x＝（x1，x2，…， xn），y＝（y1，y2，…，yn）。希尔 伯特空 间（l2；d）：l2＝｛（x1，x2，…，xn…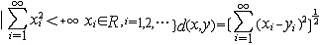）  ， 其中x ＝( x1，x2 ，…），y＝（y1，y2，…）∈l2。函数空间(ρ[0，1］，d)：C[0，1］＝｛f：f为[0，1］上的实值连续函数｝，对任意f，g∈C[0，1］，d(f，g)＝max｛｜f（x）－g（x）｜｝。 x∈[0，1］ 对度量空间（X，d）可引进拓扑结构，即以包含开球B（x，r）＝｛y∈X｜d（ x，y）＜r ｝的集为邻域定义拓扑，称为d所诱导的拓扑。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条