1) Mius minimal surface
Mius极小曲面
1.
Mius minimal surface in sphereS~n(1);
球面S~n(1)中的Mius极小曲面
2) Mbius function
Mius函数
3) Mbius
Mius变换
4) minimal surface
极小曲面
1.
Mius minimal surface in sphereS~n(1);
球面S~n(1)中的Mius极小曲面
2.
About the general parametric solutions for minimal surface equations;
关于极小曲面方程的参数通解
3.
Fairing Minimal Surface by 4-Point Interpolation Subdivision Scheme;
利用四点插值细分法构造光顺极小曲面
5) minimal surfaces
极小曲面
1.
For the min-imal case,we show that there are numerable indefinitive compact minimal surfaces without bound-ary in this 1-parameter family of surfaces and all the other innumerable indefinitive surfaces in this1-parameter family of surfaces are comp.
特别地，在极小曲面情形，证明了此单参数族的曲面中含有可数无穷多个互不相同的紧致无边极小曲面，同时还含有非可数无穷个完备非紧致的极小曲面。
2.
The theory of complete minimal surfaces in R~3 was a beautiful topic of differential geometry.
R3中完备极小曲面理论是微分几何中一个非常漂亮的一个研究课题,其中一个著名的问题是Calabi在二十世纪六十年代提出的猜想:在R3的半空间中是否存在坐标函数有界的完备极小曲面。
3.
Minimal surfaces is the surface whose average curvature is zero.
本文主要研究四元数射影空间中的特殊曲面-极小曲面。
6) minimal hypersurface
极小超曲面
1.
We consider a solutionfof a certain Dirichlet Problem on a domain in an elliptic sphereΩ,whose boundary is a minimal hypersurface and we prove a Poincare type inequality forf.
考虑椭圆球面Ω中以极小超曲面Mn-1为边界的区域上Dirichlet问题的解,得到了相应的Poincare型不等式,进一步给出了Mn-1第一特征值的下界估计。
2.
Using moving frames method,the authors classify the semi symmetric hypersurfaces in a space N n +1 ( c )( c ≠0, n ≥3) with constant curvature,and prove the connected and compact semi symmetric minimal hypersurfaces in a unit sphere S n+1 (n ≥3) are either totally geodesic or the clifford minimal hypersurfaces.
利用活动标架法给出常曲率空间Nn+ 1(c) (c≠ 0 ,n≥ 3)的半对称超曲面的分类 ,并证明了单位球面Sn+ 1(n≥ 3)上连通紧致的半对称极小超曲面或是全测地的 ,或是Clifford极小超曲面 。
补充资料：极小曲面
| 极小曲面 minimal surface 平均曲率为零的曲面。平均曲率定义为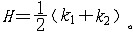：  其中k1，k2表示两个主曲率。给定一条闭曲线，可以设想蒙在这条闭曲线上的所有曲面中，有一个面积最小者，这个具有最小面积的曲面正是极小曲面。平面是仅有的极小可展曲面。除平面外，旋转极小曲面都是悬链面，直纹极小曲面都是正螺面。
|
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条