1) inverse-square central force field
平方反比有心力场
1.
Angular momentum, mechanical energy and Runge-Lenz vector are conservation in inverse-square central force field.
在平方反比有心力场中运动的质点 ,其角动量、机械能及Runge -Lenz矢量守恒 。
2) inverse square attractive(or repulsive) force
平方反比引(斥)力
3) square inverse ratio sepulsion
平方反比斥力
5) central force field
有心力场
1.
The orbital stability in the central force field;
有心力场中运动轨道的稳定性
2.
The orbit of motion in central force field is discussed and a few decision methods of the orbit stability are given.
讨论了质点运动轨道的稳定性问题,并给出了轨道稳定性的几个简明而又实用的判据,然后分析了有心力场中质点轨道的稳定性问题。
3.
By the natural and harmonious relationship between differential forms and differential equations and between differential forms and vector analysis, we discuss the properties, which are covariant under the transformation of coordinates in the framework of differential forms, of particle motion in a central force field.
通过微分形式与微分方程和向量分析之间存在的自然而协调的关系，在微分形式框架下讨论了质点在有心力场中运动的特性并得出在坐标变换下其均是协变的
6) central field
有心力场
1.
In addition,we discussed the character of these curves and the relations between Multi-knot curve and central field.
扩展了卡西尼卵形线和伯努利双纽线 ,得到所谓的多卵线和多纽线 ,并进一步讨论了这两种曲线的性质及多纽线和有心力场的关
2.
In this paper it is shown that there are two vector constants of the motion for a charged particle in the central field of force.
证明了带电粒子在有心力场中运动时有两个守恒矢量。
3.
In this paper,the symmetries of two central fields in the classical mechanics that result in closed orbits for all bound particles are discussed by using the group theory method.
本文用群论方法讨论了经典力学中导致质点作闭合轨道运动的两类有心力场的对称性，通过演算阐明了平方反比引力场和虎克定律场分别具有ＳＯ（４）和ＳＵ（３）对称性。
补充资料：有心力场
| 有心力场 central-force field 质点所受力的作用线恒通过一固定点，且其值为两点距离的函数的力场。该固定点称为力心。一个质点、一个均匀球壳或一个密度为到球心距离的函数的球体在空间产生的引力场都是有心力场。有心力场在研究行星和航天器的运动以及电子和a粒子在核电场中的运动中有广泛的应用。有心力场的一个重要性质是，质点对力心的角动量守恒，所以质点轨迹是平面曲线，且质点矢径扫过的面积速度（矢径在平面上单位时间扫过的面积）守恒。行星在太阳系中所受太阳的巨大引力远大于其他行星引力之和，故可近似地认为行星在以太阳为力心的有心力场中运动。质点在有心力场中的运动满足比奈公式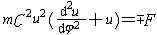：  ，式中m为质点的质量；C为面积速度的两倍；u＝1／r，r、 j为极坐标；F为质点所受的有心力，负号表示在引力作用下，正号表示在斥力作用下。用此公式，可由质点运行轨道求其所受的力，也可由力求运行轨道。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条