1) Laplacian
[lɑ:'plɑ:siən]
拉普拉斯
1.
Laplacian's Two-dimensional Principal Component Analysis and Its Application to Face Recognition
拉普拉斯二维主成分分析及其在人脸识别中的应用
2.
The gradient computation and Laplacian transformation were made for all the segmented vessel voxels.
首先,利用八叉树对体数据分块,进行血管的阈值分割和边界距离场计算时,根据每一块体数据的最大最小值与阈值的关系,只处理包含血管体素的体数据块;然后,利用血管体素的梯度值倒数和拉普拉斯变换值作为边界距离场计算的初始值;最后,利用重心法修正初始中心路径使之处于或更接近血管空腔的实际中心路径。
3.
This paper studies the universal inequalities of eigenvalues for higher order Laplacians on spherical domains.
本文研究了球面域上高阶拉普拉斯的特征值问题。
2) Laplace
[英][lɑ:'plɑ:s] [美][lə'ples]
拉普拉斯
1.
Who Established Bayesian Schools?Bayes or Laplace?;
谁开创了贝叶斯学派?——对拉普拉斯1774年一篇文章的回顾
2.
This paper is a review for Wang Youjun\'s work A Historical Research on of Laplace\'s Theory of Probability.
王幼军的《拉普拉斯概率理论的历史研究》是中国第一部概率论史研究专著。
3) Laplacian kernel
拉普拉斯核
4) Laplacian spectrum
拉普拉斯谱
1.
By means of Laplacian spectrum recursive bisection partitioning method, firstly the power network is partitioned into branch-cut form; then the branch-cut form is changed into node-split form.
利用基于拉普拉斯谱划分的递归二分法将电力网络进行支路切割,然后将支路切割转换为节点撕裂。
2.
In the present paper,the Laplacian spectrum of coronas was studied.
主要研究冠的拉普拉斯谱。
5) Laplacianfaces
拉普拉斯脸
1.
Video-based Face Recognition Using Laplacianfaces and Hidden Markov Models;
基于拉普拉斯脸和隐马尔可夫的视频人脸识别
6) Laplace solution
拉普拉斯解
补充资料：拉普拉斯
| 拉普拉斯(1749～1827) Laplace，Pierre-Simon 法国数学家 ，天文学家。法国科学院院士。1749年3月23日生于法国西北部卡尔瓦多斯的博蒙昂诺日，1827年3月5日卒于巴黎。曾任巴黎军事学院落数学教授。1795年任巴黎综合工科学校教授，后又在高等师范学校任教授。1816年被选为法兰西学院院士，1817年任该院院长。 拉普拉斯的研究领域很宽广，涉及天文、数学、物理、化学等方面的许多课题，他一生中最主要的精力是花费在天体力学上面的。他把数学当作解决问题的重要工具，而他在运用数学的同时又创造和发展了许多新的数学方法。在微分方程中有以他的名字命名的拉普拉斯方程。他在1782年就考虑过形如 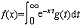 的积分方程，后来人们称它为g(t)的拉普拉斯变换。他较早地考虑了复函数求积法，并把实积分转换为复积分来计算实积分的值。在代数学中有关于行列式的拉普拉斯展开定理。他还被公认为概率论的奠基人之一。拉普拉斯的研究成果大都包括在他的3部总结性的名著中：《宇宙体系论》，其中有著名的关于太阳系起源的星云假说，因为康德也曾发表过类似的假说，所以在科学史上通常称为“康德-拉普拉斯星云说”。《天体力学》，这部5卷16册的世著实际上是I.牛顿、A.-C.克莱罗、L.欧拉、J.-L.拉格朗日以及他本人的天文学研究工作的总结和统一。《概率的分析理论》是概率论方面的一部内容丰富的奠基性著作。书中首次明确给出了概率的古典定义，系统叙述了概率论的基本定理，建立了观测误差理论（包括最小二乘法），并把概率论应用于人口统计。书中大量运用了拉普拉斯变换，生成函数和许多数学工具。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条