1) the dimension of self-similarity


自相似维数
1.
The calculation formula of the dimension of self-similarity about waste rock fragmentation was obtained through expected value of random fragmentation number and self-similarity ration.
为了探讨冒矸破碎的机理及分布状态,从分形几何学的角度建立了冒矸破碎统计自相似分形模型,并通过随机破碎个数与自相似比的数学期望,给出了冒矸破碎分形自相似维数的计算公式;最后讨论了分形维数在冒矸破碎模型中的表征情况及取值范围。
2) similar dimension


相似维数
1.
In this paper, similar dimension statistical method has been used to study the distribution of fracture zone, and the parameter is used to compare the fractures' development of several sand layers quantitatively.
运用相似维数统计法对裂缝发育带在二维平面内分布的分形特征进行研究 ,并用该定量参数进行层间裂缝发育程度的定量对比。
3) self-similar functions


自相似函数
1.
The dynamic problems under the action of instantaneous impulse loads and increasing loads pt located at the origin of the coordinates are studied respectively by the methods of self-similar functions, and the universal expressions of analytical solutions to stresses, displacements and stress intensity factors are obtained.
通过自相似函数的方法对坐标原点受到瞬时脉冲载荷、增加载荷pt作用下的动态扩展问题分别进行研究,获得了应力、位移和应力强度因子解析解的一般表达式。
2.
Analytical solution to stresses,displacements and dynamic stress intensity factors were obtained by the method of self-similar functions.
利用自相似函数的方法获得应力、位移和动态应力强度因子的解析解。
3.
The problems discussed can be easily transformed into Remann-Hilbert problems by this method,and analytical study is obtained by means of self-similar functions.
应用该法可以迅速地将所论问题转化为R iem ann-H ilbert问题,通过自相似函数的方法就可以获得解析解。
4) Hurst coefficient


自相似参数
5) self-similar function


自相似函数
1.
The universal representations of analytical solutions are obtained by the approaches of self-similar functions.
通过自相似函数的方法可以获得解析解的一般表达式。
2.
The problems discussed can be transformed into Riemann-Hilbert problems by this method, then analytical solutions are obtained by self-similar functions.
采用自相似函数的方法可以获得解析解的一般表达式。
3.
By the approaches of self-similar functions,the problems considered can be transformed into Riemann-Hilbert problems,and analytical solutions of stresses,displacements and dynamic stress intensity factors for moving crack are obtained by Muskhelishvili s method.
采用自相似函数的方法可以将所讨论的问题转化为 Riemann—Hilbert 问题,然后应用 Muskhelishvili 方法就可以得到运动裂纹的应力、位移和应力强度因子的解析解。
6) index of Self similarity


自相似指数
1.
In the present paper, the general representations for the solution are firstly derived for orthotropic elastic dynamic problems of arbitrary index of Self similarity.
首先对具有任意自相似指数的正交异性弹性动力学问题推导了解的一般表示,给出了一般解法,然后用这一方法对若干具体问题进行求解。
补充资料:流体力学相似准数
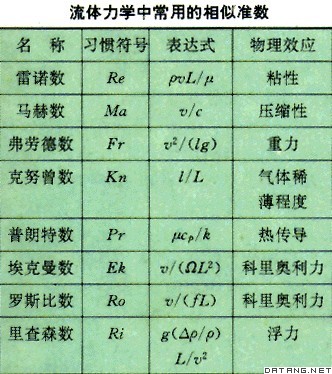
| 流体力学相似准数 fluid mechanics,similarity parameters for 两规模不同的流动保持相似所遵循的准则中出现的表征某些物理效应,由多个物理量构成的无量纲组合量。又称相似参数或无量纲参数。根据相似理论,在保持几何相似的前提下,两个规模不同的流动保持相似的条件是,所有对流动有影响的上述无量纲组合量必须保持对应相等,故它们称为相似准数。将流动的基本方程无量纲化或根据π定理,都能导出相似准数。实际流动总是受多个物理效应制约,因而可导出多个相似准数。但对某一具体流动,或涉及流动的某一具体方面,通常只有一、二个相似准数起主导作用,如粘性流动中是雷诺数,可压缩流动中是马赫数等。流体力学实验研究主要采用相似实验的方式,因此必须确定实验中有哪些相似准数起作用,哪些是主要的,应保持主要相似准数与实际流动时的相等。若实验不能保证主要相似准数相等,则必须对实验结果进行修正。例如,由于雷诺数包含了尺度因子,利用缩尺模型进行实验时,保持雷诺数与实际时的相等是非常困难的,因而对雷诺数影响比较大的实验结果(主要是阻力方面的数据)应予以修正。流体力学中常用的相似准数如下表:表中,ρ为流体密度;v为特征速度;L为特征长度;μ为粘度;c为声速;g为重力加速度;ι为气体分子平均自由程;υ为运动粘性系数;cp为定压比热容;k为热导率;Ω为流体旋转角速度;f为科里奥利参数。
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条