1) weight variable of MEOWA


MEOWA算子权向量
2) vector operator


向量算子
1.
This paper gives the vector operator roots of the matrix equation ∑=F∑F′+Q by means of the matrix s Kronecker product and vector operator vec.
以矩阵的克罗内克积和向量算子vec作为工具,给出了矩阵方程∑=F∑F′+Q的向量算子闭式解。
3) vector valued operator


向量值算子
4) vector operation and taylor series


向量算子及级数
5) one-way quantum computation


单向量子计算
6) vector-valued maximal operators


向量值极大算子
补充资料:向量
| 向量 vector 一种既有大小又有方向的量。又称矢量。在理论和实际中均广泛应用。速度、加速度、力等都是向量。 从空间中任一点出发,作一直线l,在l上取一点B,则有向线段AB就代表一个向量,记作AB或a(图1),它的大小是线段AB的长度,也称为模或绝对值,记作|a|=a,方向就是l的方向。如果另有A¢B ¢||蜛B,且指向相同,长度相等 ,就说向量AB=A¢B ¢。这种起点可以自由改变的向量常称为自由向量,当点B与A重合时,称为零向量,记作0,它的模为0,方向不确定。模为1的向量称为单位向量,向量a=b,当且仅当它们的方向相同且模相等,非零向量a与b平行或重合记为a∥b。-a是指与a方向相反模相等的向量。a与b垂直,如果它们所在直线垂直,记为a⊥b,除上面这种几何表示法以外,还常用代数方法表示向量,这种方法便于运算,便于进行有关性质的讨论。具体做法如下:在空间取定一右手坐标系(图2),把给定向量的起点放在原点,其终点为P,则a=OP,设P点在坐标系下的坐标为(x,y,z),则a={x,y,z}就是向量a的代数表示,分别称x,y,z为向量a在x轴、y轴、z轴上的分量,零向量o的三个分量均为0,即o={0,0,0}。下面介绍向量的数乘、加减法、内积、外积和混合积等运算。这些运算在代数表示法下简单明了,在几何表示法下直观,各有长处。数乘:向量a与数c相乘,得到向量ca,其模为|ca|=|c||a|,当c>0时,方向与a相同,c<0时,方向与a相反,c=0时,方向不定,得到零向量。若用代数表示法,a={x,y,z},则 ca={cx,cy,cz}。数乘满足结合律:b(ca)=(bc)a。加法:将a=OA,b=OB取在同一起点O(图3),再以OA,OB为边作平行四边形OACB,定义向量OC=c为向量a与b之和。为用代数表示法,a={x1,y1,z1},b={x2,y2,z2},则定义a+b={x1+x2,y1+y2,z1+z2},向量加法满足交换律、结合律和对数乘的分配律。向量的减法可作为加法的逆运算来定义。向量的内积(也称为点积):设a,b均不为零向量,它们的夹角为θ,则定义a·b=|a||b|cosθ,如a、b中有一个为零向量,则定义a·b=0。用代数表示法,当a={x1,y1,z1},b={x2,y2,z2}时,a·b=x1x2+y1y2+z1z2,内积满足交换律、结合律及与数乘的分配律。向量的外积:对于两个不平行的非零向量a、b,定义a×b为向量c,|c|=|a||b||sinθ|,其中θ为a与b的夹角,且c与a、b均垂直,a、b、c的指向构成右手系(图4),因为a×b仍为向量,故外积也称为向量积。用代数表示法时,a×b=c={y1z2-z1y2,z1x2-x1z2,x1y2-y1x2},其中a={x1,y1,z1} ,b={x2,y2,z2},向量的内积与外积间满足关系:(a×b)2=a2b2-(a·b)2 。向量的混合积(a×b)·c ,也记为(a,b,c)。设a={x1,y1,z1},b={x2,y2,z2},c={x3,y3,z3},则 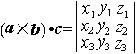
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |