1) bounded variation solution


有界变差解
1.
The relation between a class of ordinary differential equations and Kurzweil generalized ordinary differential equations is discussed on weak conditions by using Kurzweil integral,and the theorem of continuous dependence on a parameter of bounded variation solutions for the class of ordinary differential equations is established.
在很弱的假设条件下,利用Kurzweil积分讨论一类常微分方程与Kurzweil广义常微分方程的关系,在此基础上,建立了此类常微方程有界变差解对参数的连续依赖性定理。
2.
With the aid of Henstock-Kurzweil integral which encompasses the Lebesgue integral,generalized Carathéodory system x =f(t,x)is investigated and the existence theorem of the bounded variation solution for this system is obtained.
利用比Lebesgue积分更广泛的Henstock-Kurzweil积分,对广义Carathéodory系统x'=f(t,x)进行了研究,得到了该系统有界变差解的存在性定理。
3.
In this paper,the variational stability of bounded variation solutions to homogeneous linear ordinary differential equations are disscussed by using Henstock integral and Lyapunov function,the Lyapunov type theories for variation stability and variational-asymptotically stability of bounded variation solutions are established.
利用Henstock积分和Lyapunov函数,讨论了齐次线性常微分方程有界变差解的稳定性,建立了有界变差解的变差稳定性和变差渐近稳定性的Lyapunov型定理。
2) bounded Φ-variation solutions


Φ有界变差解
1.
The existence theorem for bounded Φ-variation solutions to the Caratheodory system is established by using the bounded Φ-variation function theory, which was introduced by Musielak and Orlicz.
本文借助Musielak及Orlicz等人提出的Φ有界变差函数理论,建立了Caratheodory系统在Henstock-Kurzweil积分意义下的Φ有界变差解的存在性定理。
2.
In this paper,we discuss the bounded Φ-variation solutions of the Caratheodory system by combining the theories of function of bounded Φ-variation and the Caratheodory system.
本文将Φ有界变差函数理论与Caratheodory系统结合起来,讨论了Caratheodory系统的Φ有界变差解。
3) bounded Φ-variation solution


Φ-有界变差解
1.
Bounded Φ-Variation Solutions of Kurzweil Equations;


Kurzweil方程的Φ-有界变差解
2.
The local existence theorem of bounded Φ-variation solutions for impulsive differential equations at fixed times is established.
讨论了固定时刻脉冲微分系统与Kurzweil广义常微分方程之间的关系,建立了固定时刻脉冲微分系统Φ-有界变差解的局部存在性定理。
3.
In this paper, the bounded Φ-variation function and the generalized ordinary differen- tial equation are unified, the concept of Φ-variational stability is established and the stability of the bounded Φ-variation solutions to Kurzweil equations is discussed.
本文将Φ-有界变差函数理论与Kurzweil方程理论结合起来,首次给出了Φ-变差稳定性概念,讨论了Kurzweil方程Φ-有界变差解的稳定性,建立了Φ-界变差解Φ-变差稳定性和渐近Φ-变差稳定性的Ljapunov型定理。
4) bounded variation function


有界变差
1.
A theorem on estimate of pointwise approximation of bounded variation functions defined on by the partial sums of the second Chebyshev-Fourier series is obtained,and this theorem to monotonic type continuous functions is applied.
得到了第二类Chebyshev-Fourier级数部分和对[-1,1]上有界变差函数点态逼近估计的一个定理,并把这个定理应用于单调型连续函数。
5) bounded variation


有界变差
1.
Several conclusions of bounded variation in infinite integration convergence;


有界变差在无穷积分收敛中的几个结果
2.
This paper discussed some properties of fuzzy measure,internal measure and fuzzy integration on a normal fuzzy measure space which is subadditive and has bounded variation.
讨论了次可加、具有有界变差的正规模糊测度空间上关于模糊测度、内测度及模糊积分的性质,在此基础上定义了此模糊测度空间上随机变量的条件数学期望,它是相对于经典测度空间的一个推广。
3.
A discussion is made of the continuously sufficient and necessary conditions of the bounded variation f(x)on the closed interval in the paper.
讨论了有界变差数 f(x)在闭区间上连续的充要条件以及函数 f(x)在闭区间上有有界变差的充要条件。
6) σ-boundary Variation


σ-有界变差
补充资料:有界变差函数
| 有界变差函数 bounded variation,function of 定义在区间[a,b]上,并能表为两个单调增函数之差的实值函数。属常用的函数类,它有许多好的性质,例如:有界变差函数必为有界函数;两个有界变差函数的和、差、积仍为有界变差函数;有界变差函数在[a,b]上黎曼可积;有界变差函数在[a,b]上几乎处处可导,导函数在[a,b]上勒贝格可积。此外还有,平面上由y=f(x)表示的曲线C可求长的充分必要条件是f为有界变差函数。应注意的是,连续函数不一定为有界变差函数。例如: 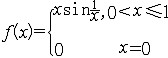 。 。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条