1) Bernoulli numbers


伯努利数
1.
The treatise here is about the history of Bernoulli numbers and two kinds of Euler numbers in both East and West, on which compare between ancient Chinese mathematics and that of western Europe has been done, and some new results are presented.
本文讨论了伯努利数、两类欧拉数的起源与发展。
3) bernoulli constant


伯努利常数
4) Bernoulli sets


伯努利集
1.
In this paper,we give two combinatorial results on Bernoulli sets over n-letter alphabet which is the partly generalization of the results by Aldo.
得到了伯努利集在n个字母情况下的两个组合性质,从而推广了Aldo de Luca相应的研究结果,同时给出了n=3时的两个推论。
5) bernoulli method


伯努利法
6) Bernoulli force


伯努利力
补充资料:伯努利数
| 伯努利数 Bernoulli numbers 18世纪瑞士数学家约翰第一·伯努利引入的一个数。设伯努利数为Bn,其定义: 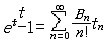 这里|t|<2π。由计算知:B 0=1,B 1= 这里|t|<2π。由计算知:B 0=1,B 1=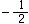 ,B 2= ,B 2=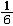 ,B 3=0,B 4 = ,B 3=0,B 4 =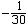 ,B 5=0, B 6= ,B 5=0, B 6=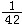 ,……。一般地,n≥1时,有B2n+1=0;n≥2时,有公式 ,……。一般地,n≥1时,有B2n+1=0;n≥2时,有公式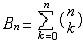 可用来逐一计算伯努利数。伯努利数在数论中很有用。伯努利数还可用于费马大定理的论证中。德国数学家E.E.库默尔证明了:当p为正规素数时,费马大定理成立。不难计算当3<p<100时,除开p=37,59,67以外 ,其余的素数都是正规素数。因此,在费马大定理的研究中,库默尔的结果是一项突破性的工作。尽管有许多判别正规素数的法则,但是,是否有无穷多个正规素数,尚未解决。而非正规素数有无穷多个,早在1915年就被人们所证明。 可用来逐一计算伯努利数。伯努利数在数论中很有用。伯努利数还可用于费马大定理的论证中。德国数学家E.E.库默尔证明了:当p为正规素数时,费马大定理成立。不难计算当3<p<100时,除开p=37,59,67以外 ,其余的素数都是正规素数。因此,在费马大定理的研究中,库默尔的结果是一项突破性的工作。尽管有许多判别正规素数的法则,但是,是否有无穷多个正规素数,尚未解决。而非正规素数有无穷多个,早在1915年就被人们所证明。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条