1) quadratic residue codes over Z_(2~k)


Z_(2~k)上的二次剩余码
2) the idempotent generator of quadratic residue codes over Z_(2~k)


Z_(2~k)上的二次剩余码的幂等元
3) cyclic codes over Z_(2~k)


Z_(2~k)上的循环码
4) quadratic residue code


二次剩余码
1.
Using the idempotent obtained one can discuss quadratic residue code over Z__2_m to see whether it is similar to the(quadra-)tic residue code over a finite field.
利用具有这些性质的幂等元可讨论环Z2m上的二次剩余码是否具有有限域上二次剩余码的性质。
5) quantum quadratic residue codes


量子码的二次剩余码
6) k th power residue


k次剩余
1.
In this paper,the author give a formula of the number of k th power residues modulo m.


给出了模m的k次剩余个数的公式 。
补充资料:二次剩余
| 二次剩余 quadratic residue 数论基本概念之一。若a、m的最大公约数为1〔记为(a,m)=1〕,m整除(x-a)〔记为x2≡ a(mod m)〕有解,则称a为模m的二次剩余(或平方剩余); 否则,称a为模m二次非剩余(或平方非剩余)。解一般二次同余式ax2+bx+c≡0(mod m)的问题可归结为解x2≡n(mod m)问题(见同余)。欧拉给出了判别条件:若p是奇素数,(a,p)=1,则a是模p的二次剩余的充分必要条件为 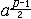 ≡1(mod p );a是模p的二次非剩余的充分必要条件为 ≡1(mod p );a是模p的二次非剩余的充分必要条件为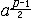 ≡-1(modp)。称{k|0<k≤m,(k,m)=1}为m的 简化剩余系。显然当m是奇素数p时,其简化剩余系令p-1个数 。若p是奇素数,a是整数,令 ≡-1(modp)。称{k|0<k≤m,(k,m)=1}为m的 简化剩余系。显然当m是奇素数p时,其简化剩余系令p-1个数 。若p是奇素数,a是整数,令 称 称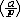 为勒让德符号。若p,q为不同的奇素数,则 为勒让德符号。若p,q为不同的奇素数,则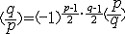
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |