1) DSP LogiCORE products


DSP逻辑内核产品
1.
SystemView by Elanix provides an easytouse visual design environment for DSP and communications applications, enabling the most efficient design to be quickly determined SystemView by Elanix is tightly integrated with the Xilinx Core Generator and DSP LogiCORE products, providing a direct path to a high performance silicon implementation for DSP application
Elanix公司的 System View与 Xilinx公司的内核产生器和 DSP逻辑内核产品紧密结合 ,提供了直接在硅芯片上实现数字处理应用的新途径。
2) logistic product


逻辑产品
1.
But logistic products have no carrier, the paper analyses characteristics of logistic products and study on its Function-Cost Analysis.
而逻辑产品没有载体,本文在分析逻辑产品特点的基础上,研究其功能成本分析问题。
3) logical product model


逻辑产品模型
1.
Complying with product configurability, a logical product model based on non-binary constraint is built.
依据产品的可配置性,提出基于非二元约束的逻辑产品模型,给出基于动态变量序的一类配置求解算法。
4) DSP C6713 core


DSP C6713内核
5) logical check


逻辑核查
1.
Ways of logical check in data management with EpiData;


EpiData用于数据管理逻辑核查功能的实现
6) logical domain core


逻辑域核
1.
By developing Wen-Syan Li s website logical domain theory,the paper proposes a website logical domain core model and logical domain mining algorithm based upon it.
通过进一步发展Wen-SyanLi等人提出的Web站点逻辑域理论,该文提出Web站点逻辑域核模型及建立在其上的逻辑域挖掘算法。
补充资料:逻辑
| 逻辑 logic 以推理形式为主要研究对象的科学。推理是以一个或几个命题为根据或理由以得出一个命题的思维过程。 推理可分为演绎推理和归纳推理。对于一个正确的演绎推理形式,不论其中的变项代入任何非逻辑词项,如果前提都是真的,则结论也是真的。在此意义上,正确的演绎推理形式有必然性(见形式逻辑)。正确的归纳推理形式却不具有必然性而只具有或然性。一个应用了正确归纳推理形式的归纳推理,其或然性的大小不仅决定于它所应用的归纳推理形式,而且还决定于它对所涉及的现象的分析和这种分析所根据的知识的可靠程度。由于有两种不同的推理,逻辑就可分为以演绎推理为主要研究对象的演绎逻辑和以归纳推理为主要研究对象的归纳逻辑。逻辑按其历史 发展的不同阶段,又可分为传统逻辑和现代逻辑。现代逻辑的主流是数理逻辑,它是形式逻辑的现代形式。 逻辑作为一门科学,不仅研究个别的正确推理形式,而且还研究各种正确推理形式之间的关系和提出关于正确推理形式的系统理论。亚里士多德的三段论理论,就是一个关于三段论的公理系统。现代逻辑则应用更加严格的形式系统的方法来研究逻辑,提出了许多关于逻辑系统的元定理和元理论。 词源 “逻辑”一词源于古希腊语 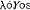 。在汉语中 ,“逻辑”这个名称是拉丁语系的logic、logik和logique的音译 。亚里士多德在定义三段论时虽然曾用过 。在汉语中 ,“逻辑”这个名称是拉丁语系的logic、logik和logique的音译 。亚里士多德在定义三段论时虽然曾用过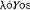 这个希腊字,但他只是在“议论”或“论证”的意义上使用它 。他没有用 这个希腊字,但他只是在“议论”或“论证”的意义上使用它 。他没有用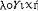 这个希腊字表示逻辑,他是应用 这个希腊字表示逻辑,他是应用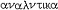 (意即分析或分析学)表示关于推理的理论。根据现有史料,公元前1世纪的 M.T.西塞罗最早用 (意即分析或分析学)表示关于推理的理论。根据现有史料,公元前1世纪的 M.T.西塞罗最早用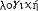 这个字表示逻辑。在中国古代和近代,曾用形名之学、名学、辩学、名理、理则学、论理学等表示逻辑。到20世纪才通用逻辑这一译名。 这个字表示逻辑。在中国古代和近代,曾用形名之学、名学、辩学、名理、理则学、论理学等表示逻辑。到20世纪才通用逻辑这一译名。不同的逻辑传统 逻辑所研究的正确推理形式及其规律,是任何正确认识和任何学科都必须应用和遵守的,因而是全人类共同的。正确地反映正确推理形式及其规律的逻辑,也是全人类共同的。在这个意义上,没有不同民族、不同阶级和不同个人的逻辑。但是,另一方面,逻辑作为一个知识体系,总是某一时代、某一民族和某些个人的产物,因而就不可避免地要带有某个时代、某个民族和某些个人的特点。因此,在逻辑发展的历史过程中,就产生了许多不同的逻辑体系并形成了3个不同的逻辑传统,即中国逻辑传统、印度逻辑传统和希腊逻辑传统。 ①中国逻辑传统。中国逻辑传统形成于先秦时期,对它的形成和发展作出重大贡献的有名家、墨家和儒家的代表人物。名家是最早出现的逻辑学派,创始人是邓析,重要的还有惠施和公孙龙。墨家的逻辑思想主要表现在《墨子》中 。儒家对中国逻辑传统的贡献主要在于它的正名理论,代表人物有孔子和荀子。秦汉以后,由于封建统治者罢黜百家、独尊儒术和其他原因,中国逻辑就很少有重大的发展。 ②印度逻辑传统。印度的各个宗教和哲学派别都有自己的逻辑理论,各派的逻辑理论既互相批评又互相促进,从而形成独特的印度逻辑传统。印度逻辑理论的主要派别,是婆罗门的正理逻辑与佛教的因明。 ③希腊逻辑传统。在世界三大逻辑传统中,希腊逻辑传统达到了最高的成就,现代逻辑就是从这一传统发展而来的。希腊传统形成于古代希腊,一直延续到近代西方。 古希腊最早出现的逻辑系统是亚里士多德的逻辑。在亚里士多德的全部逻辑著作中,包括了5个方面的内容:研究命题形式和推理形式的三段论理论;把三段论和归纳应用于辩论中的辩证推理理论;把三段论和归纳应用于科学中的科学推理理论和科学方法论;语法和语义的理论;本体论的理论。亚里士多德在他的三段论理论中已经应用了当时几何学所应用的数学方法,即应用了变项与公理方法。这是希腊逻辑传统中的一个非常重要的因素。亚里士多德还提出了模态三段论。他也用一些自明的模态三段论作为公理,以推出其他正确的模态三段论。 亚里士多德也研究了科学推理的性质及其在科学中的作用。他指出,一门科学中的科学推理,除了要求它的前提是真实的和必然的,还要求:它的前提能最后从作为这门科学出发点的直接性命题推出;它的前提相对它的结论,必须是人们更好理解的;它的前提相对于它的结论,必须是理论上在先的;它的前提必须是它的结论的原因,即必须能说明它的结论的原因。亚里士多德十分重视归纳在科学认识中的作用。他认为,人们先有关于事物的知觉,然后形成关于事物的概念,在此基础上再应用归纳就能得到作为科学的出发点的第一原则和直接性前提。 继亚里士多德之后出现的麦加拉-斯多阿学派逻辑,是古希腊逻辑的另一高峰。麦加拉-斯多阿逻辑家给希腊逻辑传统增添了重要的内容。麦加拉-斯多阿的逻辑是命题的逻辑。麦加拉-斯多阿逻辑家比亚里士多德更加明确地区别了语言表达式与它们的意义,并强调逻辑规律只是根据表达式的意义。 中世纪逻辑是希腊逻辑发展的重要阶段。欧洲中世纪经院逻辑家主要是从阿拉伯人那里继承了古希腊的逻辑成果 。因此,阿拉伯逻辑也是中世纪逻辑的一个组成部分。古希腊逻辑大约在公元后5世纪开始传入叙利亚,约9世纪巴格达成了当时阿拉伯地区研究逻辑的中心,出现了巴格达学派。巴格达学派主要是注释和讲述亚里士多德逻辑 。亚里士多德《工具论》中的6篇、他的《修辞学》、《诗学》和波尔费留的《亚里士多德范畴引论》,是巴格达学派学习逻辑必读的逻辑九书。 大约12~15世纪,欧洲经院逻辑继承和发展了古希腊和阿拉伯的逻辑思想,建立了完整的经院逻辑体系,从而对希腊逻辑传统作出了重要的贡献。经院逻辑明确区分了范畴词与非范畴词。范畴词是指谓确定的对象的语词,如“人”。非范畴词本身并不指谓任何对象,但它们和范畴词联结起来,使范畴词以某种方式指谓某种对象 ,例如 ,“所有的”、“有的”、“非”等。经院逻辑还应用范畴词定义了命题和推论的形式和内容。经院逻辑提出了关于词项的性质的理论,特别是指代的理论。这是一种涉及量词与语言层次的理论 ,是经院逻辑中很有独创性的部分。在模态逻辑方面,经院逻辑明确区分了命题模态和事物模态。如果一个模态词作为整个命题的谓词,那么它就是命题模态;如果一个模态词作为命题中的谓词的形容词,那么它就是事物模态。经院逻辑家认为,逻辑是关于思想或意义的科学,特别是关于非范畴词的意义的科学。逻辑同语法、修辞、算术、音乐、建筑学和天文学一样,是神学的支柱或婢女,但却不是神学的一部分。 随着16世纪实验科学的出现,人们对逻辑这门科学产生了新的要求。F.培根认为,当时流行的演绎逻辑已不能满足科学发展的需要。他企图创造一种新的逻辑作为科学的新工具。他认为,演绎只能阐明已经发现的东西,只能判定由一些思想推出另一个思想的过程是正确的或错误的。只有归纳才能发现真理,才能发现事物的规律。培根的归纳方法不同于简单枚举的归纳,是一种设计实验并由实验结果找出事物规律的方法。他提出了有名的三表法:出现表,罗列所研究的现象出现的所有情况;不出现表,罗列所研究的现象不出现的所有情况;程度表,罗列所研究的现象在程度上的各种变化。通过这3个表就可找出所研究的现象的原因和规律 。 J.S.密尔继承和发展了培根的归纳法,他提出了求因果五法,即契合法、差异法、契合差异并用法、剩余法和共变法。密尔五法是培根三表的发展,密尔不仅把五法看作指导实验的方法,而且把五法看作归纳推理的模式。 R.笛卡尔则从另一个角度批判当时的演绎逻辑,他强调数学的方法作为研究科学的新方法。他认为,理智有直观与推理两种活动,在直观中我们应形成清楚明确的概念,然后应用推理特别是数学的推理从这些清楚明确的概念得出必然的结论。他在其《指导理智的规则》和《论方法》中,提出许多关于得到清楚明确的概念和进行正确推理的具体规则。 I.康德认为,在普通逻辑即形式逻辑之外,还有先验逻辑。先验逻辑分为先验分析(或分析学)和先验辩证法两个部分。在先验分析中,他分析了知识即先天综合判断中的先天因素。他认为,知性中有12个先天范畴,经验和知识是知性把这些先天范畴应用于感性材料的结果。他把这12个范畴分为4组:量范畴、质范畴、关系范畴和模态范畴。相应于这4组范畴,他提出知性的4个原则,即直观公理、知觉预期、经验类比和经验的思想公设。先验辩证法是分析理性超出了经验范围所产生的谬误。 G.W.F.黑格尔发展了康德先验逻辑的理论。全面地和系统地叙述了思想范畴的辩证发展。黑格尔认为思想范畴也就是存在范畴。因此,黑格尔的逻辑也就是他的绝对唯心论的认识论和本体论。这样的逻辑完全不同于亚里士多德开创的演绎逻辑和培根开创的归纳逻辑。 现代逻辑 现代逻辑的主流是数理逻辑,此外也包括非经典的逻辑。现代归纳逻辑和自然语言逻辑也属于现代逻辑的范围。 ①数理逻辑。数理逻辑是一门边缘性的科学。它一方面应用数学方法研究逻辑问题,另一方面又应用逻辑的成果去研究数学的基础和方法。这两方面的研究,是紧密联系、互相促进和逐步提高的。经过近百年来的发展,数理逻辑已具有非常丰富的内容(见数理逻辑)。 ②非经典逻辑。布尔逻辑代数、罗素和怀特海的逻辑演算以及希尔伯特和阿克曼的逻辑演算,都是二值的外延逻辑。这些逻辑体系中的命题或命题形式,只能有而且必须有真和假这二值之一 。其中的逻辑词项 ,如“不”、“或”、“和”、“如果……,那么……”、“所有的”、“有的”等,都是真值函项的或外延性的语词。这样的二值外延逻辑演算或逻辑体系,被称为经典的逻辑演算或逻辑体系。非经典的逻辑演算或逻辑系统,就是非二值的或非外延的逻辑演算或逻辑系统。模态逻辑、多值逻辑、道义逻辑、认知逻辑、时态逻辑等都属于非经典逻辑的范围。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条