1) Multi-frame blind deconvolution


多帧盲去卷积
2) blind deconvolution


盲去卷积
1.
A weighted total variation algorithm was proposed for solving some blind deconvolution problems,and then we got the existence of energy functional minimum and educed corresponding thermal flow.
为了进一步观察此算法的实效性,与全变差盲去卷积模型的实验结果进行了比较。
3) blind deconvolution


盲目去卷积
1.
Based on the Shalvi-Weinstein criterion,a super-exponential algorithm for Raman spectra blind deconvolution is proposed.
基于Shalvi-Weinstein盲目去卷积标准,提出了一种拉曼光谱盲目去卷积的超指数收敛算法,可以同时从观测数据估计真实光谱数据与仪器的响应函数,且具有超指数的收敛速度。
2.
In order to restore the turbulence-degraded image efficiently,a single frame blind deconvolution image restoration algorithm with .
为了对湍流退化图像进行有效复原,提出了一种基于贝叶斯理论的单帧双重循环盲目去卷积图像复原算法,并对该算法的快速实现进行了研究,最后还进行了稳健性分析与测试。
3.
For the restoration of the degraded images caused by aero-optics effects of atmospheric turbulence, this paper presents an effective algorithm of multi-resolution blind deconvolution based on two frames of degraded images, in which the PSFs can be estimated by use of the two degraded images under the condition of the degraded models being unknown.
为了有效地恢复气动光学效应退化图像 ,该文提出了一种基于两帧退化图像的多分辨率盲目去卷积复原算法 。
4) iteration blind deconvolution


迭代盲目去卷积
5) multi-channel blind deconvolution


多通道盲反卷积
1.
The multi-channel blind deconvolution model is analyzed for vibration signals of rolling bearings,and the Blind Least Mean Square method is discussed.
分析了滚动轴承振动信号的多通道盲反卷积模型。
6) multichannel blind deconvolution


多通道盲解卷积
1.
Then, two multichannel blind deconvolution algorithms are obtained, which are the deconvolution versions corresponding to the Amari’s natural gradient algorithm and Cardoso’s Equivariant adaptive algo.
通过FIR滤波器矩阵代数将盲源分离算法扩展为多通道盲解卷积算法,得到了多通道盲解卷积的自然梯度算法和等变自适应算法。
补充资料:卷积
| 卷积 convolution 分析数学中一种重要的运算。设f(x), g(x)是R1上的两个可积函数,作积分: 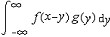 可以证明,关于几乎所有的x∈(-∞,∞) ,上述积分是存在的。这样,随着x的不同取值 ,这个积分就定义了一个新函数h(x),称为f与g的卷积,记为h(x)=(f *g)(x)。容易验证,(f *g)(x)=(g *f)(x),并且(f *g)(x)仍为可积函数。这就是说,把卷积代替乘法,L1(R1)1空间是一个代数,甚至是巴拿赫代数。 可以证明,关于几乎所有的x∈(-∞,∞) ,上述积分是存在的。这样,随着x的不同取值 ,这个积分就定义了一个新函数h(x),称为f与g的卷积,记为h(x)=(f *g)(x)。容易验证,(f *g)(x)=(g *f)(x),并且(f *g)(x)仍为可积函数。这就是说,把卷积代替乘法,L1(R1)1空间是一个代数,甚至是巴拿赫代数。卷积与傅里叶变换有着密切的关系。以 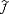 (x) , (x) , (x)表示L1(R)1中f和g的傅里叶变换,那么有如下的关系成立:(f *g)∧(x)= (x)表示L1(R)1中f和g的傅里叶变换,那么有如下的关系成立:(f *g)∧(x)=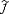 (x)· (x)· (x),即两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换。这个关系,使傅里叶分析中许多问题的处理得到简化。 (x),即两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换。这个关系,使傅里叶分析中许多问题的处理得到简化。由卷积得到的函数(f *g)(x),一般要比f,g都光滑。特别当g为具有紧支集的光滑函数,f 为局部可积时,它们的卷积(f *g)(x)也是光滑函数。利用这一性质,对于任意的可积函数 , 都可以简单地构造出一列逼近于f 的光滑函数列fs(x),这种方法称为函数的光滑化或正则化。 卷积的概念还可以推广到数列 、测度以及广义函数上去。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条