1) CAD dimension driving technique


CAD尺寸驱动技术
1.
CAD dimension driving technique was used to solve the workspace, and parameters to describe the workspace and orientation of the moving platform were defined.
采用CAD尺寸驱动技术求解了机构的工作空间,定义了描述工作空间及动平台姿态变化的参数,对10种机构的工作空间及姿态变化范围进行了比较,分析了运动副布置对于3-SPR并联机构工作空间及姿态变化的影响。
2) dimension driven


尺寸驱动
1.
In order to obtain the solution for motion simulation and kinematic analysis of a parallel machine tool without the construction of mathematical model,a method of using assembly constraint and dimension driven function of CAD software was presented.
为了不建立数学模型完成并联机床机构的运动仿真和运动学分析,提出综合利用CAD软件所具有的装配约束和尺寸驱动功能实现运动仿真和运动学分析的方法。
2.
In order to obtain the solution for mapping NC code of a parallel machine tool from virtual axis space to real axis space without the construction of mathematical model, a method of using assembly constraint and dimension driven function of CAD software was presented.
为了有助于并联机床数控系统和仿真系统的开发 ,克服建立数学模型实现机床数控代码虚实映射计算的缺点 ,文章提出了综合利用CAD软件的装配约束和尺寸驱动功能来实现虚实映射的方法。
3.
By using the constraint and dimension driven concept in CAD software, some type of simulation for planar mechanisms is created.
提出用 CAD约束和尺寸驱动技术分析平面机构的运动 。
3) dimension drive


尺寸驱动
1.
It narrates two ways of developing plat for SolidWorks,using VB to make parametric design——dimension drive method and program drive method.
介绍了SolidWorks软件的优点;叙述了以SolidWorks为开发平台,应用VB进行参数化设计的两种方法——尺寸驱动法和程序驱动法。
2.
Based on relationship and principle of dimension drive,using CAXA entity design to establish the reusable parametric intellectual pixels.
基于关联和尺寸驱动原理,使用CAXA实体设计,建立可重用的参数化智能图素,调用CAXA实体设计的二次开发函数以及C++标准模板库,通过参数名建立了不同特征尺寸之间的映射关系,以此来驱动相应的尺寸值,在CAXA实体设计上成功实现了自动装配设计功能,并给出应用实例原型。
3.
In this paper,we use modularization,relation,dimension drive and so on technologies,through CAXA Solid Design creating reuseable parameter parts and calling it s second-development interfaces,successfully realize no-constrain smart assembly design function on CAXA Solid Design.
论文基于模块化、关联、尺寸驱动等技术,通过CAXA实体设计建立可重用的参数化模块并调用其二次开发接口,在CAXA实体设计上成功实现了无约束方式的自动装配设计功能,并给出应用的实例原型。
4) dimension-driven


尺寸驱动
1.
And based on the graph, the parametric design is realized by dimension-driven approach, which includes creation and search of dimension chain and topology chain.
本文围绕二维参数化草图技术,系统地研究了如何向二维草图添加结构约束和尺寸约束,并在图的基础上,通过建立和搜索尺寸链和拓扑链进行尺寸驱动来实现参数化设计。
2.
In this paper,the problems of intelligent dimension-driven in 2-D parametric plotting are discussed.
讨论了利用智能化尺寸驱动技术实现二维参数化绘图中的问题。
3.
In this paper, the problem of intelligent dimension-driven in 2-D parametric plotting is discussed.
讨论了二维参数化绘图中的智能化尺寸驱动问题。
5) Dimension driving


尺寸驱动
1.
This paper provided a 2D/3D parametric modeling and dimension driving drafting method by using AutoLISP language on AutoCAD R14 software, and provided a primary method of FEM programming.
介绍了在AutoCADR1 4平台上以AutoLISP语言为工具进行二维、三维机械结构的参数化几何设计和实现图形的尺寸驱动 ,并提出有限元分析编程的初步方法 。
2.
This paper analyzes the characteristic of non standard hydraulic cylinders, discourses upon the general scheme of the CAD of non standard hydraulic cylinders, and emphasizes on discussing the implementing method of the dimension driving module and intensity checking module.
分析了非标准液压缸的特点 ,论述了非标准液压缸CAD总体设计方案 ,着重分析讨论非标准液压缸CAD系统中尺寸驱动模块和强度校核模块的实现方法。
6) size drive


尺寸驱动
1.
This system consists of 8 moulds:design selection,structure module calculation,parts model building,assembles,parts graphic transformation,size drive,database management and help.
该系统由方案选择、结构设计计算、零件建模、装配、零件图转换、尺寸驱动、数据库管理、帮助等8个模块组成。
补充资料:CAD技术在特殊尺寸检测中的应用
在实际的生产加工中,经常会涉及到特殊尺寸的测量和检测,由于曲面检测有一定的难度,因此会出现一些加工误差。本文介绍了应用CAD曲面造型技术和CAD测量技术处理曲面加工误差的两种方法,误差计算方法简单直观,易于掌握和操作。计算过程人为干预少,计算结果准确率高,是将专业技术人员从繁琐复杂的计算中解放出来的一种简便方法。
一、问题的提出
计算机辅助设计技术即CAD技术,由于其具有高度专业性、强大的计算功能、形象逼真及图形绘制准确等特点,在现代工程设计中得到了广泛应用。而在我们的实际研究工作中,还将CAD技术应用于机械零件加工特殊尺寸检测中。
我们接到了一个加工任务,首先建立该零件的三维数字模型,如图1所示。
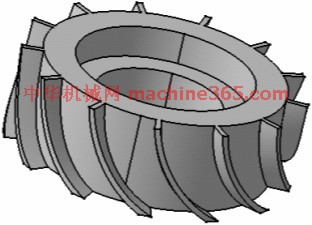
图1 零件的三维数字模型
该零件的加工难点是零件圆周上的齿面。在设计图上,是在圆柱面的展开图上进行标注的,齿面在圆柱面上的投影为一条圆弧曲线,如图2所示。
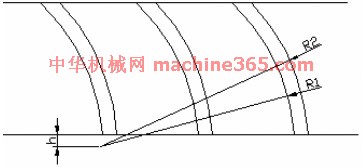
图2 齿面在圆柱面上的投影
在逐点计算加工的刀具路径后,进行加工编程,然后在加工中心上加工该零件的齿面。要求齿面加工的外观质量令委托方满意,并出具齿面加工的尺寸检验报告。如何检验齿面的加工精度,成了摆在我们面前的难题。
二、检验的难度
从图1中可以看出,该齿面为空间曲面,无法用一般工程技术人员所掌握的数学公式及理论去描述。
1. CAD曲面造型原理
任意空间曲面都可以看作是无数点的集合。
如图3所示,在V方向任意截面上选择M+1个点为特征顶点,用最小二乘积逼近方法可生成一条曲线,该曲线即为B样条曲线。同样,在V方向的不同截面上可生成一组(N+1)条B样条曲线,在U方向的不同截面也生成一组(M+1)条B样条曲线。两组B样条曲线的直积可求得B样条曲面,该曲面即为任意复杂空间曲面。
图3 B样条曲面
其数学表达式为:
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条