1) Tsallis entropy


Tsallis
1.
New thresholding method using two-dimensional Tsallis entropy;


一种新的基于二维Tsallis熵的阈值方法
2) tsallis entropy


Tsallis熵
1.
Image segmentation based on 2D Tsallis entropy with improved pulse coupled neural networks;
基于二维Tsallis熵的改进PCNN图像分割
2.
Tsallis entropy and nonextensive statistical mechanics;


Tsallis熵与非广延统计力学
3.
Fast SAR image segmentation method based on grey Tsallis entropy


基于灰色Tsallis熵的SAR图像快速分割
3) time-dependent Tsallis entropy


时变Tsallis熵
1.
Two estimating algorithms,time-dependent Tsallis entropy(E_(TsEn)) and time-dependent approximate entropy(E_(ApEn)),are provided to analyze the dynamic transformation of cognitive event-related potential complexity in Stroop tasks.
提供了两种分析认知事件相关电位(ERP)复杂度动态变化的估计算法———时变Tsallis熵(ETsEn)和时变近似熵(EApEn),并将其应用于分析Stroop任务中ERP的动态复杂度。
4) Tsallis– Havrda– Charvát entropy


Tsallis–Havrda–Charvát熵
5) Tsallis statistics


Tsallis统计
1.
Tsallis statistics was used to fit the probability density functions and the result showed that they were fitted very well.
对一维FPU模型中类似湍流行为进行了数值模拟,得到不同条件下速度差的概率密度函数,并利用Tsallis统计对其进行拟合,发现两者符合得非常好。
6) Tsallis Divergence


Tsallis散度
补充资料:熵
| 熵 entropy 描述热力学系统的重要态函数之一。熵的大小反映系统所处状态的稳定情况,熵的变化指明热力学过程进行的方向,熵为热力学第二定律提供了定量表述。 为了定量表述热力学第二定律,应该寻找一个在可逆过程中保持不变,在不可逆过程中单调变化的态函数。克劳修斯在研究卡诺热机时,根据卡诺定理得出,对任意循环过程都有 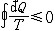 ,式中 ,式中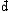 Q是系统从温度为T的热源吸收的微小热量,等号和不等号分别对应可逆和不可逆过程。可逆循环的 Q是系统从温度为T的热源吸收的微小热量,等号和不等号分别对应可逆和不可逆过程。可逆循环的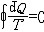 表明存在着一个态函数熵,定义为 表明存在着一个态函数熵,定义为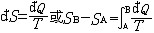 对于绝热过程 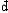 Q=0,故 Q=0,故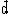 S≥0,即系统的熵在可逆绝热过程中不变,在不可逆绝热过程中单调增大。这就是熵增加原理。由于孤立系统内部的一切变化与外界无关,必然是绝热过程,所以熵增加原理也可表为:一个孤立系统的熵永远不会减少。它表明随着孤立系统由非平衡态趋于平衡态,其熵单调增大,当系统达到平衡态时,熵达到最大值。熵的变化和最大值确定了孤立系统过程进行的方向和限度,熵增加原理就是热力学第二定律。 S≥0,即系统的熵在可逆绝热过程中不变,在不可逆绝热过程中单调增大。这就是熵增加原理。由于孤立系统内部的一切变化与外界无关,必然是绝热过程,所以熵增加原理也可表为:一个孤立系统的熵永远不会减少。它表明随着孤立系统由非平衡态趋于平衡态,其熵单调增大,当系统达到平衡态时,熵达到最大值。熵的变化和最大值确定了孤立系统过程进行的方向和限度,熵增加原理就是热力学第二定律。能量是物质运动的一种量度,形式多样,可以相互转换。某种形式的能量如内能越多表明可供转换的潜力越大。熵原文的字意是转变,描述内能与其他形式能量自发转换的方向和转换完成的程度。随着转换的进行,系统趋于平衡态,熵值越来越大,这表明虽然在此过程中能量总值不变,但可供利用或转换的能量却越来越少了 。 内能 、 熵和热力学第一、第二定律使人们对与热运动相联系的能量转换过程的基本特征有了全面完整的认识。 从微观上说,熵是组成系统的大量微观粒子无序度的量度,系统越无序、越混乱,熵就越大。热力学过程不可逆性的微观本质和统计意义就是系统从有序趋于无序,从概率较小的状态趋于概率较大的状态。 在信息论中,熵可用作某事件不确定度的量度。信息量越大,体系结构越规则,功能越完善,熵就越小。利用熵的概念 ,可以从理论上研究信息的计量 、传递 、变换 、存储。此外,熵在控制论、概率论、数论、天体物理、生命科学等领域也都有一定的应用。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条