1) network traffic


网络业务流
1.
A great deal of research on telecommunication network indicate that the network traffic is self-similar in essentially(represents long range dependence on correlation function).
讨论了当前网络业务流的特性;分析了现有的自相似业务流模型。
2.
In this paper, we propose a new multifractal wavelet model for the increasing network traffic and video traffic on the Internet.
针对当前Internet上日益复杂的网络业务流和视频流 ,文章提出了一种新的多重分形小波模型 。
3.
With the rapid development of the Internet, modeling and control of network traffic become more and more important.
论文研究了几类网络业务流——视频会议业务流、视频影片业务流以及一般的网络业务流的建模和分析问题,以及一类网络业务流——Web业务流的控制问题。
2) network service flow design


网络业务流设计
1.
This paper deals with the necessity and feasibility of the application of data excavation in network service flow designs, probes into the whole process in which the application of data excavation is conducted while network services being analyzed.
本文论述了数据挖掘技术在网络业务流设计中应用的必要性和可行性,探讨了在进行网络业务分析时运用数据挖掘技术的全过程,并指出该分析是以业务为分析单位,运用该方法可以从业务角度对网络状况和网络行为进行分析。
4) network traffic


网络业务
1.
Network Traffic Modeling and Forecasting Based on Time Series Analysis;


基于时序分析的网络业务分析与预报
2.
Characteristics Analysis and Performance Evaluation of Network Traffic;


网络业务特性分析与性能评价
3.
An algorithm of classifying network traffic based on ensemble neural networks is proposed in this pa- per.
针对目前计算机网络业务流管理问题,提出了一种基于复合神经网络的网络业务分类方案。
5) service network


业务网络
1.
Research and Realization of Telecom Service Network and Platform;


电信业务网络和业务平台研究及实现
2.
The operators must redesign their operation strategy,business model,operation paths and even the service network and the organization.
因此,电信运营企业应通过整合内外资源,科学构建业务网络,合理进行组织变革,并通过成功的产品管理,利用业务平台提供满足客户个性化需求的产品,实现电信运营企业的成功转型,最终保证企业的长期盈利能力。
6) network traffic statistical characteristic


网络业务流量统计特性
补充资料:网络流
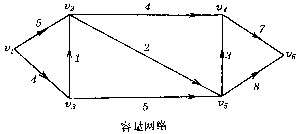
| 网络流 network flows 图论中的一种理论与方法,研究网络上的一类最优化问题。1955年,T.E.哈里斯在研究铁路最大通量时首先提出在一个给定的网络上寻求两点间最大运输量的问题。1956年,L.R.福特和D.R.富尔克森等人给出了解决这类问题的算法,从而建立了网络流理论。所谓网络或容量网络指的是一个连通的赋权有向图D=(V、E、C),其中V是该图的顶点集,E是有向边(即弧)集,C是弧上的容量。此外顶点集中包括一个起点和一个终点。网络上的流就是由起点流向终点的可行流,这是定义在网络上的非负函数,它一方面受到容量的限制,另一方面除去起点和终点以外,在所有中途点要求保持流入量和流出量是平衡的。如果把下图看作一个公路网,顶点v1…v6表示6座城镇,每条边上的权数表示两城镇间的公路长度。现在要问:若从起点v1将物资运送到终点v6去,应选择那条路线才能使总运输距离最短这样一类问题称为最短路问题。如果把上图看作一个输油管道网,v1表示发送点,v6表示接收点,其他点表示中转站,各边的权数表示该段管道的最大输送量。现在要问怎样安排输油线路才能使从v1到v6的总运输量为最大这样的问题称为最大流问题。
最大流理论是由福特和富尔克森于1956年创立的,他们指出最大流的流值等于最小割(截集)的容量这个重要的事实,并根据这一原理设计了用标号法求最大流的方法,后来又有人加以改进,使得求解最大流的方法更加丰富和完善。最大流问题的研究密切了图论和运筹学,特别是与线性规划的联系,开辟了图论应用的新途径。 最大流问题仅注意网络流的流通能力,没有考虑流通的费用。实际上费用因素是很重要的。例如在交通运输问题中,往往要求在完成运输任务的前提下,寻求一个使总运输费用最省的运输方案,这就是最小费用流问题。如果只考虑单位货物的运输费用,那么这个问题就变成最短路问题。由此可见,最短路问题是最小费用流问题的基础。现已有一系列求最短路的成功方法。最小费用流(或最小费用最大流)问题,可以交替使用求解最大流和最短路两种方法,通过迭代得到解决。 目前网络流的理论和应用在不断发展,出现了具有增益的流、多终端流、多商品流以及网络流的分解与合成等新课题。网络流的应用已遍及通讯、运输、电力、工程规划、任务分派、设备更新以及计算机辅助设计等众多领域。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条