1) nonlinear Schroedinger equation with varying coefficients
变系数非线性薛定谔方程
2) The (higher-order) nonlinear Schr(o|¨)dinger equation with variable coefficients
变系数(高阶)非线性薛定谔方程
3) nonlinear schrodinger equation
非线性薛定谔方程
1.
First,we analyzed nonlinear schrodinger equation by split-step Fourier transform method(SSFM).
主要研究高阶色散对光孤子传输的影响,首先通过分步傅里叶法(SSFM)分析非线性薛定谔方程,然后综合考虑高阶色散对光孤子共同作用的结果,得出三阶色散对孤子传输的影响独立于其它的效应,也使得孤子脉冲在其中一个边沿产生不为零的衰减振荡,并且使脉冲展宽,严重影响了孤子的传输。
2.
In this paper,several study methods on PMD are analyzed,such as Jones matrix,Stokes vector and the coupled nonlinear Schrodinger equation.
主要分析讨论了PMD的几种研究方法:琼斯矩阵法、斯托克斯空间法和耦合非线性薛定谔方程。
3.
The method is based on the construction of a certain complete integrable finite-dimensional dynamical system, Whose solutions determine the exact solutions of nonlinear Schrodinger equation.
通过构造一个完全可积的有限维动力系统及其求解，我们获得了描述光学纤维中正群速色散脉冲传播的非线性薛定谔方程的精确解。
4) nonlinear Schrdinger equation
非线性薛定谔方程
1.
The nonlinear Schrdinger equation with time-dependent linear potential is discussed,and the exact N-soliton solutions are presented by employing the Darboux transformation method.
考虑含时线性势非线性薛定谔方程 ,通过 Darboux变换给出该方程的 N-孤子解 ,由此得到一孤子解和二孤子解的精确表达形式 ,并讨论孤子解的性质和相互作
2.
In this article, the authors investigate the non existence of a class of homoclinic orbits to the Stokes waves for a perturbed nonlinear Schrdinger equation.
本文讨论了一个扰动非线性薛定谔方程对于Ｓｔｏｋｅｓ波的一类同宿轨道，证明了这类轨道是不存在
5) nonlinear Schrdinger equation
非线性薛定谔方程
1.
Based on the modified nonlinear Schrdinger equation expressing the solitons transmission,studied are the interaction of solitons and their dispersion-managed transmission in dispersion-shifted fibers under Kerr coefficient distributing randomly by making use of symmetrical slit-step Fourier numerical method.
从描述孤子传输的修正非线性薛定谔方程出发,利用对称分步傅里叶方法,在伴随Kerr系数随机扰动的色散位移光纤中,对孤子间的相互作用及其色散管理传输进行了数值研究。
2.
Through solving the nonlinear Schrdinger equation,the propagation variation of B integral of Nd:glass in high power laser system is numerically simulated.
通过对非线性薛定谔方程的求解,数值模拟了高功率激光系统中钕玻璃的B积分传输规律,并理论分析了B积分对光脉冲的波形和频谱的影响,详细介绍了几种消除B积分影响的方法。
3.
A family of exact solutions of the one-dimensional nonlinear Schrdinger equation is derived, which describes the dynamics of a bright soliton in Bose-Einstein condensates with the time-dependent interatomic interaction in an expulsive parabolic potential.
给出了一个一维非线性薛定谔方程的严格解,它描述了在一个排斥势中随时间变化的原子间相互作用的玻色-爱因斯坦凝聚的一个亮孤子的动力学。
6) higher-order nonlinear Schrodinger equation
高阶非线性薛定谔方程
1.
By using the fractional transformation method, the exact solutions of the higher-order nonlinear Schrodinger equation are obtained which included Jacobian elliptic function solution and new solitary wave solution.
本文基于分数变换原理,研究了用于描述飞秒光脉冲传输的高阶非线性薛定谔方程,得到了它的各种包络型Jacobian椭圆函数双周期解和新型亮孤波解。
补充资料：薛定谔方程
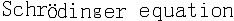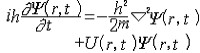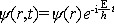薛定谔方程 E.薛定谔提出的量子力学基本方程 。建立于 1926年。它是一个非相对论的波动方程。它反映了描述微观粒子的状态随时间变化的规律，它在量子力学中的地位相当于牛顿定律对于经典力学一样，是量子力学的基本假设之一。设描述微观粒子状态的波函数为Ψ（r，t），质量为m的微观粒子在势场U（r，t）中运动的薛定谔方程为  。在给定初始条件和边界条件以及波函数所满足的单值、有限、连续的条件下，可解出波函数Ψ（r，t）。由此可计算粒子的分布概率和任何可能实验的平均值（期望值）。当势函数U不依赖于时间t时，粒子具有确定的能量，粒子的状态称为定态。定态时的波函数可写成 式中Ψ（r）称为定态波函数，满足定态薛定谔方程 ，这一方程在数学上称为本征方程，式中E为本征值，是定态能量，Ψ（r）又称为属于本征值E的本征函数。量子力学中求解粒子问题常归结为解薛定谔方程或定态薛定谔方程。薛定谔方程广泛地用于原子物理、核物理和固体物理，对于原子、分子、核、固体等一系列问题中求解的结果都与实际符合得很好。 薛定谔方程仅适用于速度不太大的非相对论粒子，其中也没有包含关于粒子自旋的描述。当计及相对论效应时，薛定谔方程由相对论量子力学方程所取代，其中自然包含了粒子的自旋。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条