1) linearity transformation matrix


线性变换矩阵
3) f-matrixes of linear transform


线性变换的f-矩阵
4) corresponding matrix of linear transformation


线性变换对应矩阵
5) ray transfer matrix


光线变换矩阵
6) transformation matrix


变换矩阵
1.
This paper applies the array manifold interpolation wideband direction finding algorithm on uniform linear array,and gives other two methods of seeking transformation matrix.
文中把阵列流行内插宽带测向算法应用到均匀线阵上,并给出了求变换矩阵的另外两种方法。
2.
At the same time, the transformation matrix M ct between the camera and the vehicle has been calculated.
建立了摄像机坐标系 ,轮式移动机器人车体坐标系以及目标物体 (世界坐标系 )之间的位姿关系模型 ,着重论述了摄像机与轮式移动机器人车体之间的坐标变化关系 ,并求出了其变换矩阵Mct。
3.
The method generates the resulting transformation matrix.


针对野战战术三维环境原型系统BIT-VBFS的开发过程中所遇到的将模型从右手坐标系移植到左手坐标系的问题,提出了一种在不同三维坐标系之间寻找对应的变换矩阵的一般性方法,这种方法得到的是对于变换的转换矩阵,所以在对模型进行实际的转换时并没有增加计算的复杂度。
补充资料:线性变换
| 线性变换 linear transformation 线性代数研究的一个对象,向量空间到自身的保运算的映射。例如,对任意线性空间V,位似σk:a 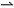 ka是V的线性变换,平移则不是V的线性变换,若a1,…,an是V的基,σ(aj)=a1ja1+…+anj(j=1,2,…,n),则称 ka是V的线性变换,平移则不是V的线性变换,若a1,…,an是V的基,σ(aj)=a1ja1+…+anj(j=1,2,…,n),则称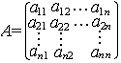 为σ关于基{a:}的矩阵。对线性变换的讨论可藉助矩阵实现。σ关于不同基的矩阵是相似的。Kerσ={a∈V|σ(a)=θ}(式中θ指零向量)称为σ的核,Imσ={σ(a)| 为σ关于基{a:}的矩阵。对线性变换的讨论可藉助矩阵实现。σ关于不同基的矩阵是相似的。Kerσ={a∈V|σ(a)=θ}(式中θ指零向量)称为σ的核,Imσ={σ(a)|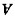 a∈V}称为σ的象,是刻画σ的两个重要概念。 a∈V}称为σ的象,是刻画σ的两个重要概念。对于欧几里得空间,若σ关于标准正交基的矩阵是正交(对称)矩阵,则称σ为正交(对称)变换。正交变换具有保内积、保长、保角等性质,对称变换具有性质:〈σ(a),β〉=〈a,σ(β)〉。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条