1) geometric average


几何平均数
1.
Two lemmas of trigonometric inequality can be deduced by the application of the principle that arithmetic average is greater than or equal to geometric average.
利用算术平均数大于或等于几何平均数的不等式,将一个三角不等式的两个引理进一步做出推广,并得到另一种类型的三角不等式。
2.
In order to emphasize the influence of over-irrigation or insufficient irrigation on irrigation uniformity,this paper put for- ward the concept of distribution uniformity coefficient based on geometric average,which is defined as the ratio between geometric average of the depth of partial measuring points and arithmetic average of all points.
为突出局部灌溉不足或灌溉过量对均匀性的影响程度,提出了基于几何平均数分布均匀系数的概念,将其定义为部分测点水深几何平均值与所有测点算术平均值的比值。
2) geometrical average


几何平均数
1.
A new functional inequality was established as one of the two applications,which could prove the notable inequality that the geometrical average is no more than the algebraic average,and could also prove its related forms.
建立了一个新的泛函不等式,作为应用,给出了著名不等式“几何平均数不大于算术平均数”及其推广形式的一种新证明。
2.
In this paper, the relation X≥ X G≥ X H between arithmetic average X, geometrical average X G and harmonic average X H of positive number X i>0 (i=1,2,…,n) is proved.
证明了正数xi>0 (i =1 ,2 ,… ,n) ,的算术平均数x,几何平均数xG,调和平均数xH 间的x≥ xG ≥xH 关系 。
3) geometric mean


几何平均数
1.
The practical usage of weighted mean in cotton had been expounded through calculated method of circular cone position in cotton bolls and mean of boll weight,and the practical usage of geometric mean,the growth per cent of plant height a day had been expounded through analysing exponential increasing phase of plant height in cotton.
以棉株结铃的平均圆锥体部位、平均铃重的计算方法 ,阐明了加权平均法在棉花上的实际应用及注意事项 ;通过对棉花株高指数增长阶段的分析 ,阐明了棉花株高日生长率作为几何平均数的实际应
4) weighted geometrie average


加权几何平均数
5) geometric average index number


几何平均指数
6) geometric crosses


几何平均数交叉
补充资料:几何平均数
| 几何平均数 geometric mean n个正数乘积的n次算术根。给定n个正数 a1,a2,…,an,其几何平均数为 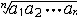 。特别是,两个正数a,b的几何平均数c= 。特别是,两个正数a,b的几何平均数c=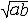 是a与b的比例中项。任意n个正数a1,a2 ,…,an的几何平均数不大于这n个数的算术平均数,即 是a与b的比例中项。任意n个正数a1,a2 ,…,an的几何平均数不大于这n个数的算术平均数,即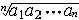 ≤ ≤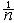 (a1+a2+…+an) 。这个不等式在研究其他不等式或极值等问题时常起特殊作用。 (a1+a2+…+an) 。这个不等式在研究其他不等式或极值等问题时常起特殊作用。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条