1) hypotheses-test method


假设-检验方法
2) Bayes hypothesis test method


Bayes假设检验方法
4) Hypothesis test


假设检验
1.
Some advice in hypothesis test teaching about health statistics;


卫生统计学假设检验教学中的几点思考
2.
Hypothesis Test of the Factor of Safety of Slope and Its Application in Engineering;


边坡安全系数的假设检验法及其工程实例分析
3.
Object detection algorithm based on background motion compensation and hypothesis test;


背景运动补偿和假设检验的目标检测算法
5) hypothesis-test


假设检验
1.
Clarifying a Common Mistake in Using Hypothesis-test;


对假设检验使用中一个常见错误的澄清
2.
Based on planning the magnetic experiment of seven different experimental conditions,the effect of magnetic treatment with three different degrees of density was investigated by using hypothesis-test theory to check the data of Sedimentation in the magnetic field.
通过设计7组不同条件的磁化实验,考察了不同磁场强度的磁场对污泥沉降性能的影响;并利用数理统计分析中的假设检验原理将所得试验数据进行了均值假设检验,结果表明:磁场的确对污泥沉降性能有影响,其影响效果为:平行磁化优于垂直磁化,平行磁化中磁场强度越大效果越好。
3.
Based on the principles of hypothesis-test in terms of Beyasian statistics,the article analysized and replied to psychological researchers main criticisms about the classical hypothesis-test method.
根据假设检验原理的贝叶斯统计的表达方式分析和回应了心理学中对传统的假设检验方法的主要批评。
6) hypothesis testing


假设检验
1.
Sample size estimation and hypothesis testing of assessing equivalence/noninferiority for paired binary data;
配对二项数据等效性/非劣效性评价的样本含量估计和假设检验
2.
Automatic recognition of airfield runways based on hypothesis testing in SAR images;


基于假设检验的SAR图像机场跑道自动识别
3.
Multiple fading Kalman filter based on hypothesis testing;


一种基于假设检验的多重渐消卡尔曼滤波
补充资料:假设检验
| 假设检验 hypothesis testing 一种基本的统计推断形式。又称统计假设检验。数理统计学的一个重要分支。假设是指关于总体分布的一项命题 。例如 ,一群人的身高服从正态分布N(μ ,σ2),则命题“这群人的平均身高μ≤1.70(米)”是一个假设 。又如,有一批产品,其废品率为p,则“废品率p≤0.03”这个命题也是一个假设。假设是否正确, 要用从总体中抽出的样本进行检验,与此有关的理论和方法,构成假设检验的内容。 设A是关于总体分布的一项命题,所有使命题A 成立的总体分布构成一个集合H0,称为原假设(常简称假设)。使命题A不成立的所有总体分布构成另一个集合H1 ,称为各择假设。如果H0可以通过有限个实参数来描述,则称为参数假设,否则称为非参数假设(见非参数统计)。如果H0(或H1)只包含一个分布,则称原假设(或备择假设)为简单假设,否则为复合假设。对一个假设H0进行检验,就是要制定一个规则,使得有了样本以后 ,根据这个规则可以决定是接受它(承认命题A正确),还是拒绝它(否认命题A正确)。这样, 所有可能的样本所组成的空间(称为样本空间),被划分为两部分  A和 A和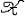 R( R(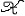 A的补集),当样本x∈ A的补集),当样本x∈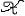 R时,接受假设H0 ;当x∈ R时,接受假设H0 ;当x∈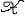 R时,拒绝H0 。集合 R时,拒绝H0 。集合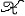 R常称为检验的拒绝域, R常称为检验的拒绝域,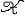 A称为接受域。因此选定一个检验法 ,也就选定一个拒绝域 ,故常把检验法本身与拒绝域 A称为接受域。因此选定一个检验法 ,也就选定一个拒绝域 ,故常把检验法本身与拒绝域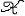 R 等同起来。 R 等同起来。J.奈曼与E.S.皮尔森合作,从1928年开始,对假设检验提出了一项系统的理论。他们认为,在检验一个假设H0时可能犯两类错误: 第一类错误是真实情况为H0成立,但判断H0不成立,犯了“以真为假”的错误。第二类错误是H0 实际不成立,但判断它成立,犯了“以假为真”的错误。通常人们不希望轻易拒绝H0。例如工厂的产品一般是合格的 ,出厂进行抽样检查时不希望轻易地被认为不合格,即犯第一类错误的概率不能太大,于是在限定犯第一类错误的概率不超过某个指定值a(称为检验水平)的条件下,寻求犯第二类错误尽可能小的检验方法。 基于奈曼-皮尔森理论及统计决策理论,提出了一些优良性准则,来比较为检验同一假设而提出的各种检验。较重要的有一致最大功效(UMP)准则和无偏性准则, 把统计决策理论中容许性、同变性、贝叶斯决策、最小化最大等概念引进到假设检验中来,得到容许检验、同变检验、贝叶斯检验和最小化最大检验等。寻求在一定准则下的最优检验是十分困难的,何况这种最优检验有时并不存在。于是提出了若干依据直观的推理法,得到相应的拒绝域,其中最重要的是似然比法。 似然比检验是运用与最大似然法类似的原理,得到似然比检验法。用似然比法导出的重要检验有:①U检验。若总体服从正态分布,方差已知,检验总体均值是否等于(大于等于或小于等于)某个值时,使用U检验。②t检验。若总体服从正态分布,方差未知,检验总体均值是否等于(大于等于或小于等于)某个值时,使用t检验。③F检验。若两个总体均服从正态分布,检验这两个总体的方差是否相等(大于等于或小于等于)时,使用F检验。在方差分析中广泛使用F检验。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条