1) m geometric number sequence


m等比数列
2) m geometric series


m等比级数
3) geometrical sequence


等比数列
1.
This article discussed the new qualities and the prove of geometrical sequence and arithmetical sequence.
介绍了等比数列和等差数列的两个新性质及其发现、证
4) double equal ratio series


双等比数列
1.
The definition of double equal ratio series is given in the paper and the general term and formula of former n terms are given.
给出了双等比数列的定义和三等比数列概念,推证出双等比数列和三等比数列的通项公式和前n项和公式,最后给出了三等比数列的概念、通项公式和前n项和公式。
5) three equal ratio series


三等比数列
1.
In the end,conception of the three equal ratio series, general term and formula of former n terms are foun
给出了双等比数列的定义和三等比数列概念,推证出双等比数列和三等比数列的通项公式和前n项和公式,最后给出了三等比数列的概念、通项公式和前n项和公式。
6) geometric-arithmetic sequence


等比差数列
1.
In this paper, the sum of geometric-arithmetic sequences is given, and their simple applacations are discussed.
讨论了等比差数列的求和并由此得到几个恒等式。
补充资料:等比数列
| 等比数列 geometric sequence 从第二项起每一项与前一项的比等于同一个数的数列。又称几何数列。相邻两项的比称为等比数列的公比,如果用q表示等比数列a1,a2,…,an…的公比,那么  等比数列的通项公式是an=a1qn-1,用a1和q也可将等比数列写成a1,a1q1…,a1qn-1,…(a1≠0,q1≠0)。 等比数列的通项公式是an=a1qn-1,用a1和q也可将等比数列写成a1,a1q1…,a1qn-1,…(a1≠0,q1≠0)。等比数列的前n项的和Sn可以用a1和q表为 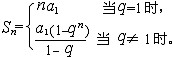 由 由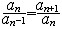 得 到 得 到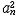 =an-1·an+1,从而有 =an-1·an+1,从而有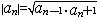 ,可知 等比数列从第二项起,每项的绝对值等于前后两个相邻项绝对值的几何平均值。 ,可知 等比数列从第二项起,每项的绝对值等于前后两个相邻项绝对值的几何平均值。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条