1) asymmetric free vibration


非对称自由振动
1.
In this paper, the transfer matrix method for the asymmetric free vibration of the circular (annular) plates with variable thickness on Winkler foundation is presented.
本文提出了Winkler地基上变厚度圆(环)板非对称自由振动的传递矩阵法。
2) Non-symmetry vibration


非对称振动
3) non symmetric autooscillations


非对称自振汤
4) symmetric and anti-symmetric stretching


对称和非对称伸缩振动
5) non-linear free vibration


非线性自由振动
1.
Planar non-linear free vibration analysis of stay cable considering the effects of flexural rigidity;
考虑抗弯刚度影响的斜拉索面内非线性自由振动分析
6) Nonlinear free vibration


非线性自由振动
1.
The nonlinear free vibration problems of symmetrical laminated skew plates are studied.


分析了具有夹紧或简支边界条件的对称角铺设斜扳的非线性自由振动问题;分别给出了满足各种边界条件的单模式的挠度表达式,并且利用伽辽金法时上述斜板的振动进行单模式分析,进而导出了时间函数的非线性常微分方程——杜芬方程。
2.
Based on the Hamilton principle,the control equations of the nonlinear free vibration on elastic foundation beam under the uniform temperature rise are obtained in this paper and the nonlinear partial differential equations are converted into a set of ordinary ones by using Kantorovich averaging procedure.
基于Hamilton原理,得到了弹性地基粱在均匀升温作用下的非线性自由振动控制方程。
3.
Based on the control equations of the nonlinear free vibration on elastic foundation beam under the uniform temperature rise,the nonlinear partial differential equations are converted into a set of ordinary ones by using Kantorovich averaging procedure.
基于弹性地基梁在均匀升温作用下的非线性自由振动控制方程,运用Kantorovich平均法将非线性偏微分方程转化成一组常微分方程,考虑不可移夹紧边界条件,采用打靶法得到了一阶屈曲位形下的前四阶振型的数值结果。
补充资料:自由振动
| 自由振动 free vibration 系统受初扰动后不再受外界激励时所作的振动。例如单自由度的弹簧振子,其振子质量为m,弹簧的刚度为k,且阻尼可以忽略,则其振动微分方程为mx+kx=0。其解为x=Asin(ωnt+j),式中x为位移;t为时间; 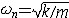 为角频率,它与初始条件无关而取决于系统的参数,也称固有频率 ;A、j分别为振幅和初相位,由振子的初位移x0和初速度 为角频率,它与初始条件无关而取决于系统的参数,也称固有频率 ;A、j分别为振幅和初相位,由振子的初位移x0和初速度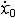 确定: 确定: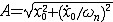 ;j=arctg(ωnx0/ ;j=arctg(ωnx0/ )( )(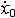 ≥0),j=π+arctg(ωnx0/ ≥0),j=π+arctg(ωnx0/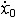 )( )(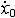 <0)。单自由度系统的无阻尼自由振动是简谐运动,其周期T 和频率f为:T=1/ f=2π <0)。单自由度系统的无阻尼自由振动是简谐运动,其周期T 和频率f为:T=1/ f=2π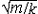 。在无阻尼自由振动的过程中,系统的动能和势能不断地相互转换,且机械能守恒;其振幅决定于系统在起振的时候所具有的能量,且大小保持不变。有阻尼的自由振动参见衰减振动。 。在无阻尼自由振动的过程中,系统的动能和势能不断地相互转换,且机械能守恒;其振幅决定于系统在起振的时候所具有的能量,且大小保持不变。有阻尼的自由振动参见衰减振动。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条