1) combinational mathematics/WZ method


组合数学/WZ方法
2) WZ method


WZ方法
1.
The Bailey4F3 identity,Vandermonde identity and Li-shanlan identity have been proved by WZ method.
利用WZ方法证明Bailey4F3恒等式、Vandermonde恒等式和李善兰恒等式成立。
3) the combined constant method


组合常数方法
1.
The article gives a lot of Bohr s theory of the Atomic Physics simplely by the combined constant method.
本文用组合常数方法简捷地给出了荡然物理学中玻尔理论的一系列结果。
4) Combination count method


组合计数方法
5) δ-combinatorial counting method


δ-组合计数方法
6) Combination method by weighing parameter


权函数组合方法
补充资料:组合数学
| 组合数学 combinatorial mathematics 以任意一组离散性事物按照一定规则安排或配置的方法为主要研究内容的数学分支。具体解决以下4个问题:①满足一定条件的安排是否存在。②在确知解存在的前提下,确定一切可能的安排个数。③给出所有可能的安排。④当对不同的安排有优劣标准时,求出最好的安排。简称存在、计数、安排、优化问题。起源于数学消遣和游戏。中国神话传说,神龟背驮洛书献给德国费马恩海峡桥大禹,上面记载着治国道理。洛书图相当一个3阶方阵,各行依次为4,9,2;3,5,7;8,1,6。其每行每列及两对角线元素之和均为15。这种图也称幻方。13世纪后期杨辉《续古摘奇算经》给出了3~10阶幻方,称幻方为纵横面,那么,是否对任意自然数n都存在n阶幻方?对每个n存在多少个n阶幻方?如何构作?这就是组合数学研究的问题之一。18世纪L.欧拉提出的36名军官问题是一个趣味数学题。用数学语言叙述即是否存在两个正交的6阶拉丁方。欧拉认为不存在6阶正交拉丁方,这个问题直到20世纪初才得到证明。再如19世纪中期的柯克曼15名女生散步问题被推广为一般柯克曼系列,至今未彻底解决,尽管组合数学历史悠久,但长期以来发展缓慢,最近几十年随着计算机科学、规划论、试验设计等学科的发展,刺激了组合数学的发展,使之有了更强的生命力,也使以往不敢问津的计算量庞大的大型问题有了解决的可能。关于计数的基本公式有:n个不同元素中取k个的排列数 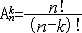 ;n个不同元素中取k个的组合数 ;n个不同元素中取k个的组合数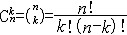 ;n个不同元素分成r组,使第i组固定包含ki个元素 ;n个不同元素分成r组,使第i组固定包含ki个元素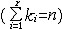 的分组方法数为 的分组方法数为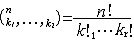 。 。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条