1) dynamic fractal dimension
动态分维数
1.
In this paper , the method of dynamic fractal dimension is presented, and sudden change in low tide level series of the Caoe River is analyzed by making use of such fractional theory The result indicates that this method is effective and utility to recognize the sudden change which is led by man or nature in tide level time serie
本文提出了动态分维数的计算方法，并应用此方法对曹娥江低潮位序列中的突变成份进行了分析。
2) Multidimensional Dynamic Parameters
多维动态参数
1.
Hierarchical Bayes Fusion Estimation for Multidimensional Dynamic Parameters;
多维动态参数的多层Bayes融合估计
3) Three-dimensional dynamic quasi-function
三维动态拟函数
4) Multidimensional data sets
多维动态数据
5) mathematics dynamic thinking
数学动态思维
1.
Effects of mathematics dynamic thinking in advanced mathematics teaching;
高等数学教学中体现数学动态思维的作用
6) 3D dynamic segmentation
3维动态分段
1.
In this paper,a novel lane-based 3D dynamic segmentation approach,shortly 3DDS,is proposed.
本文提出了基于实际车道的3维动态分段方法,以3维空间中的实际车道带作为基准,建立基于"弧段-距离-车道序号"的线性参考,显著提高了定位精度,提出了基于点序规则和基于语义规则的描述方法,实现了交通设施和交通事件灵活逼真的表达。
补充资料：分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段，总长度变为 3×4／3＝4 英尺；每一次变换使总长度变为乘以4／3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。 计算分形维数的公式是 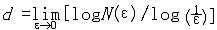 ，式中ε是小立方体一边的长度， N （ε）是用此小立方体覆盖被测形体所得的数目，维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ，覆盖一根单位 长度的线 段所需 的数目要 N （ε）＝1／ε2，覆盖一个单位边长的正方形，N(ε)＝（1／ε）2 ，覆盖单位边 长的立方体，N （ε）＝（1／ε）3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d＝1.2618，谢尔宾斯基海绵的维数d＝ 2.7268。对于无规分形，可用不同的近似方法予以计算，也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条