1) simplication of mathematical model


数学模型简化
2) simplified activated sludge process models


简化数学模型
1.
In order to promote the simplified activated sludge process models from the operation, the optimization must be used to enhance the simulation precision.
为了从控制运行的角度促进简化数学模型的应用 ,必须借助其它优化手段进一步提高预测精度。
3) mechanical simplified model


力学简化模型
1.
Using mechanical simplified model the strength of a steam tube rotary dryer rotor system is checked.
采用力学简化模型对 1台旋转列管式干燥机转子系统的各部件进行了强度校核 ,结果表明 ,各危险部位应力小于许用应力值 ,挠度与实测值相符。
4) simplified mechanical model


简化力学模型
1.
Three dimensional finite element method is used to calculate the structural dynamic properties, and the principle of equivalent dynamic properties is adopted to modify the simplified mechanical model of arch sluice.
利用三维有限元方法计算的结构动力特性与简化结构动力特性相等的原则修正弧形闸门简化力学模型 ,并确定了等效的弧形闸门三维简化结构模型和系统参数。
2.
With the rheological property of magnetorheological(MR)fluids in the presence of applied magnetic field and in the different shear strain rate as well as the mechanical principium of MR damper in the mix mode,a simplified mechanical model with four indeterminate coefficients is developed.
基于磁流变液体在不同磁场和剪切率下流变特性和磁流变阻尼器在混合模式下的力学原理,推导出包含四个待定系数的磁流变阻尼器简化力学模型。
5) reduced mechanical model


简化力学模型
1.
Based on the dynamic characteristics obtained with three dimension finite element method,the reduced mechanical model and parameters of lift ship structure can be modified and obtained.
利用三维有限元方法计算的结构动力特性和简化结构的动力特性相等的原则修正升船机结构简化力学模型 ,并确定了等效的升船机简化结构模型和系统参数 。
6) reduced chemical kinetics


简化化学动力学模型
1.
A reduced chemical kinetics including 20 species and 16 global reactions was obtained by reducing the detailed kinetics for ethylene combustion with the method of quasi-steady state approximation(QSSA).
采用"准稳态"方法,从乙烯燃烧的详细化学反应动力学模型出发,建立了包含20个组分和16步总包反应的简化化学动力学模型。
补充资料:如何简化手工编程中的数学处理
众所周知,数控机床程序编制的方法有两种:手工编程与自动编程。手工编程仍被广泛地应用于形状较简单的点位加工及平面轮廓加工。而手工编程中有一个既关键又繁琐的环节就是图形的数学处理,即通常要计算出加工轮廓的各基点或节点坐标。传统的计算方法就是建立数学方程式,解方程组,以求各关键点的坐标。这个过程对编程人员来说既耗时又容易出错。
随着绘图软件AutoCAD应用的普及,在手工编程过程中,我们可以利用AutoCAD的INQUARY(查询)、CALCULATE(计算)等命令快速、准确地求出各点的坐标,以代替复杂的数学运算。下面以一些实例来介绍具体的操作方法。
例如要编写如图1所示零件的数控加工程序,必须求出零件轮廓中各基点(如图2所示的A、B、C、D、E、F、G)的坐标值,如果用数学方法处理,则难度比较大,而且很繁琐。下面介绍如何利用AutoCAD2000得到各基点的坐标值。
下拉菜单TOOLS→MOVE UCS→鼠标左键拾取编程原点O;
或者,下拉菜单TOOLS→NEW UCS→ORIGIN→鼠标左键拾取编程原点O。
第三步:下拉菜单TOOLS→INQUIRY→ID POINT→鼠标左键拾取A点,则在命令行(COMMAND)处显示A点在编程坐标系中的坐标值,即求得编程所需的数据。用同样的方法可得到其他各点(B、C、D、E、F、G)的坐标值和圆弧圆心点的坐标值。
或者,下拉菜单TOOLS→INQUIRY→LIST→鼠标左键分别拾取A、B、C、D、E、F、G各点,则显示出各点的坐标值。
同理,对于分层切削、行切法、环切法、以及处理刀具半径的补偿问题等,都可以先用AutoCAD中的OFFSET命令对零件轮廓进行适当的偏移,生成所需的刀具加工轨迹,再用上述的方法可求出各编程点的坐标值,提高手工编程的效率和准确性。
随着绘图软件AutoCAD应用的普及,在手工编程过程中,我们可以利用AutoCAD的INQUARY(查询)、CALCULATE(计算)等命令快速、准确地求出各点的坐标,以代替复杂的数学运算。下面以一些实例来介绍具体的操作方法。
例如要编写如图1所示零件的数控加工程序,必须求出零件轮廓中各基点(如图2所示的A、B、C、D、E、F、G)的坐标值,如果用数学方法处理,则难度比较大,而且很繁琐。下面介绍如何利用AutoCAD2000得到各基点的坐标值。
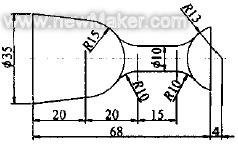
图1零件的数控加工程序

图2 零件图
下拉菜单TOOLS→MOVE UCS→鼠标左键拾取编程原点O;
或者,下拉菜单TOOLS→NEW UCS→ORIGIN→鼠标左键拾取编程原点O。
第三步:下拉菜单TOOLS→INQUIRY→ID POINT→鼠标左键拾取A点,则在命令行(COMMAND)处显示A点在编程坐标系中的坐标值,即求得编程所需的数据。用同样的方法可得到其他各点(B、C、D、E、F、G)的坐标值和圆弧圆心点的坐标值。
或者,下拉菜单TOOLS→INQUIRY→LIST→鼠标左键分别拾取A、B、C、D、E、F、G各点,则显示出各点的坐标值。
同理,对于分层切削、行切法、环切法、以及处理刀具半径的补偿问题等,都可以先用AutoCAD中的OFFSET命令对零件轮廓进行适当的偏移,生成所需的刀具加工轨迹,再用上述的方法可求出各编程点的坐标值,提高手工编程的效率和准确性。
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条