1) Rayleigh-Ritz energy method


Rayleigh-Ritz变分法
2) Rayleigh-Ritz energy principle


Rayleigh-Ritz能量变分法
3) Rayleigh-Ritz method


Rayleigh-Ritz法
1.
Their precursor Rayleigh-Ritz method and Galerkin method were introduced,the calculation example and comparison of two methods were presented,which had some reference value.
从力学问题出发来介绍计算力学中流行的两类方法:有限元法及加权参数法并以比较,同时介绍其前身Rayleigh-Ritz法与Galerkin法,并给出算例对这两种方法进行比较,具有一定的参考价值。
4) Rayleigh-Ritz method


Rayleigh-Ritz方法
1.
A geometrically nonlinear model accounting for imperfect buckling behaviour of a stayed column was formulated using the Rayleigh-Ritz method,and then validated,using the finite element method.
考虑有几何缺陷支撑柱的屈曲性能,采用Rayleigh-Ritz方法对几何非线性模型公式化,并通过有限元方法进行验证。
5) rayleigh-ritz modal method


Rayleigh-Ritz模态法
6) piece wise Ritz method


分片Ritz法
1.
A piece wise Ritz method to obtain a precise and valid solution used to analyze laminated shell structure is developed.
为了对层合壳体结构进行准确和有效的分析 ,给出了基于分片参数曲面描述的适用于层合壳体结构分析的分片Ritz法。
补充资料:变分法
| 变分法 calculus of variations 研究泛函的极值的方法。泛函就是函数的函数,给定一个函数集合Y,若对Y中的每一函数y按某一确定的规则J有一确定的实数J [y] 与之对应,就说在集合Y上给定了一个泛函J。若泛函J在Y中的y0处取的值J[y0]是J在Y中所有的y 处所取值J [y]中的最大(小)的一个 ,则说J [ y0]是最大(小)值,y0称为最大(小)值函数。设Y′是Y中在 y0附近的函数组成的子集,若J[ y0 ]是J 在Y′上取的最大(小)值,则称J[y0 ]是极大(小)值,而y0称为极大(小)值函数。极大(小)值统称极值,极大值函数和极小值函数统称极值函数。变分法的核心问题就是求泛函的极值函数和相应的极值。
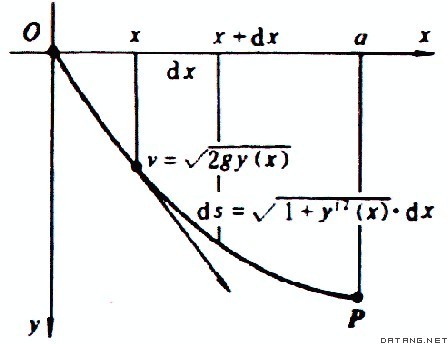
变分法的第一个著名例子是最速降曲线问题,它是由约翰第一·伯努利在1696年以挑战的口吻向当时的数学家提出的。设O和P是铅直平面 xO y内高度不同的两点,一质点在重力作用下从O点沿一曲线滑落到P点,假定无摩擦和其他阻力,问曲线呈何形状时其滑落的时间最短?设滑落曲线方程为y=y(x),由能量守恒定律和弧长公式可知所需时间为 
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
||
| ©2011 dictall.com | ||