1) canonical 3 D quadric surface equation


标准三维二次曲面方程
2) general 3 D quadric surface equation


一般三维二次曲面方程
1.
Using the method of least square, the parameters of the general 3 D quadric surface equation are solved by the coordinates of measured points.
该方法首先用被测点的坐标值 ,由最小二乘法获得测量坐标系下的一般三维二次曲面方程的参数 ,然后经过坐标变换得到标准方程的参数 ,再把它与设计的参数相比较 ,并可以由获得的标准方程重构出被测物体的曲面图形。
3) two dimensional quadric


二维二次曲面
4) n-dimensional quadratic surface


n维二次曲面
1.
We on study tangent hyperplane of n-dimensional quadratic surface by using the characteristic root,we give a necessary and sufficient condition for plane to be the tangent hyperplane of n-dimensional quadratic surface.
利用特征根研究n维二次曲面的切超平面问题,给出平面为n维二次曲面的切超平面的充要条件。
5) quadric coordinates


二次曲面坐标
6) quadratic curve equation


二次曲线方程
1.
Getting a new method to classification and simplification of the quadratic curve equation.
通过对二次曲线方程配方变形,利用直线与二次曲线相交时参数t的几何意义,以及仿射变换的性质,得到了二次曲线方程分类与化简的一种新方法,从而解决了二次曲线方程通过坐标系的平移、旋转进行分类、化简运算复杂,通过不变量进行化简,无法画出图形的具体位置等问题。
补充资料:二次曲面
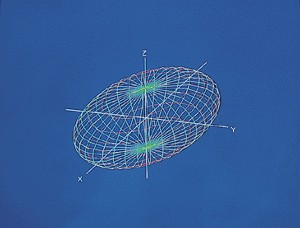
| 二次曲面 second-degree surface 在三维坐标(x、y、z)下三元二次代数方程对应的所有图形的统称。最常见的二次曲面是球面和直圆柱面及直圆锥面。此外,二次曲面还包括椭球面、双曲面(又分为单叶双曲面和双叶双曲面)和抛物面(又分为椭圆抛物面和双曲抛物面,后者又称马鞍面)。它们的大致形状,包括对称性,与各坐标面的交线 ,以及与坐标面平行的平面的截线(见图)。椭球面在3个对称轴上截得的线段,称为它的轴。当三个轴长相等时即为球面。当两个轴长相等时,它是由平面上的椭圆绕其对称轴旋转而成的旋转椭球面,一般椭球面实际是一个压扁了的旋转椭球面,它是二次曲面中仅有的一类限制在有限范围内的封闭曲面。平面上的双曲线分别绕它的虚轴和实轴旋转,得到旋转单叶双曲面和旋转双叶双曲面。平面上的抛物线绕它的对称轴旋转得到旋转抛物面。它们分别是上述几类曲面的特殊情形,压扁了就得到一般的形状。探照灯的反射镜和卫星电视天线常做成旋转抛物面的形状。当表示二次曲面的一个方程,能分解为两个一次方程的乘积时,这个二次曲面就退化成两个或相交或平行或重合的平面。
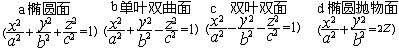
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
||||||||||||||||
| ©2011 dictall.com | ||||||||||||||||